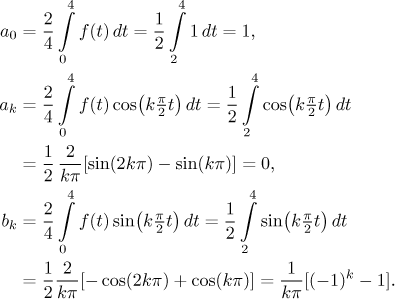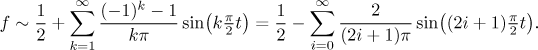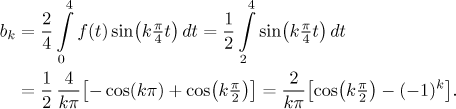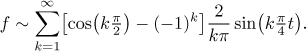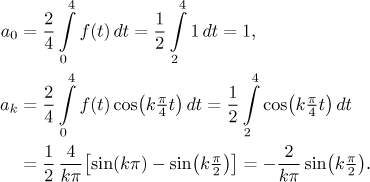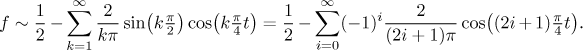Expanding in (sine, cosine) Fourier series: Methods survey
Question: Find the Fourier series for a function
f (t)
that is either
T-periodic
or given on some interval of the form
[a,a + T ).
Find the sum of this series.
Solution: First determine the frequency
ω = 2π/T
and then find coefficients by evaluating integrals
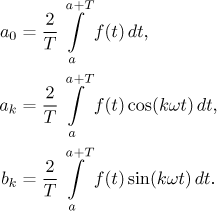
The Fourier series is then obtained by writing
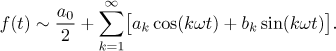
If f is nice enough (see
Jordan's conditions), you
can determine the sum of the resulting Fourier series. First, draw the
T-periodic
function f (either it was given as such or it was given on a suitable
interval, then draw its periodic extension). Then, at every point of
discontinuity, draw a dot at the level that is the average of the left and
right value there. This is the sum of the Fourier series.
Note: The coefficient a0 is actually given by the same
formula as the other ak, so we could just specify one
formula. However, for k = 0 the cosine becomes
1 and in practice we therefore evaluate a0 separately from
the other integrals anyway. Thus it is convenient to put it aside as a
special case.
Question: Find the sine Fourier series for a function
f (t)
that is given on some interval of the form
[0,L ).
Find the sum of this series.
Solution: The sine series will be based on an odd extension with
period T = 2L.
First determine the frequency
ω = 2π/T = π/L.
Then find coefficients bk as above but with L
in place of T, set
a0 and ak equal to zero and write
the series exactly as above.
If f is nice enough (see
Jordan's conditions), you
can determine the sum of the resulting Fourier series. First, draw the given
function. Second, extend the graph also to the interval
(−L,0)
in such a way that the resulting function is odd (flip the given graph about
both axes). Then draw the
T = 2L-periodic
extension of this odd function and handle points of discontinuity exactly as
above.
Question: Find the cosine Fourier series for a function
f (t)
that is given on some interval of the form
[0,L ).
Find the sum of this series.
Solution: The cosine series will be based on an odd extension with
period T = 2L.
First determine the frequency
ω = 2π/T = π/L.
Then find coefficients a0 and ak
as above but with L in place of T,
set bk equal to zero and write
the series exactly as above.
If f is nice enough (see
Jordan's conditions), you
can determine the sum of the resulting Fourier series. First, draw the given
function. Second, extend the graph also to the interval
(−L,0)
in such a way that the resulting function is even (flip the given graph about
the y-axis).
Then draw the T = 2L-periodic
extension of this even function and handle points of discontinuity exactly as
above.
It is often possible to improve the resulting series by using these handy
formulas.
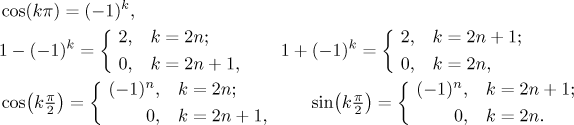
Example: Find the Fourier series, the sine Fourier series and the
cosine Fourier series for the function
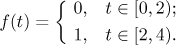
This function can be extended to a function with period
T = 4, thus the frequency is
ω = π/2.
We find the coefficients:
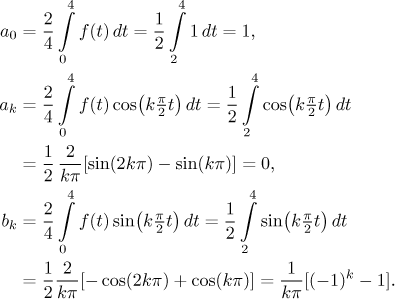
Thus we get the series
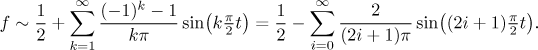
We noticed that in the series, all even coefficients are zero and odd ones are
−2, so we rewrote it accordingly.
The sine and cosine series have L = 4,
T = 8, and
ω = π/4. The sine series has
ak = 0
and
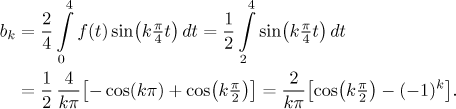
Thus the sine Fourier series is
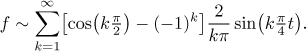
The cosine Fourier series has
bk = 0
and
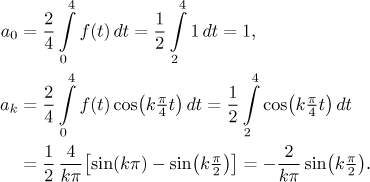
Thus the cosine Fourier series is
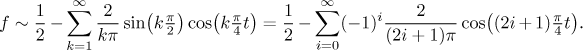
Now we determine the sums of the above three series. In the following
picture there are six graphs. The first is the periodic extension of the
given function and the second is the sum of the Fourier series by Jordan's
criterion. The third graph is the odd periodic extension and then there is
the sum of the sine Fourier series. Finally, the fifth graph is the even
periodic extension and then the sum of the cosine Fourier series.
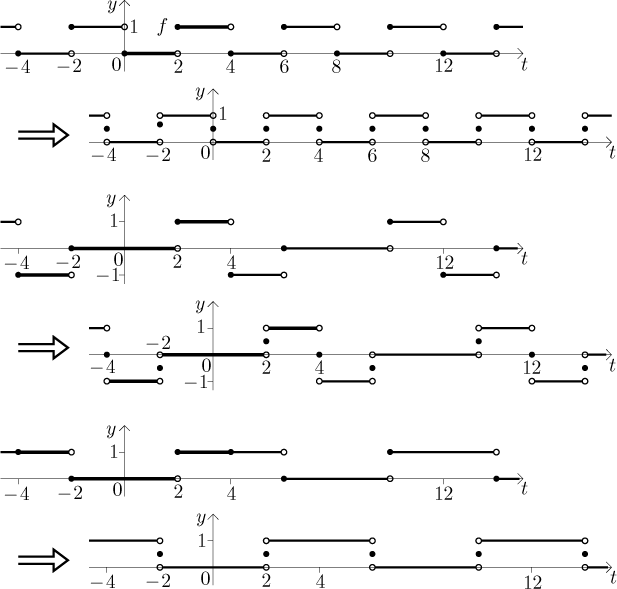
Note that the Fourier series has the form of 1/2
plus a sine series. Indeed, if we take the periodic extension of f
and move it down by 1/2, we get an odd function whose Fourier
series necessarily features only sines (and thus it is also its sine Fourier
series).
Back to Methods Survey - Series
of functions
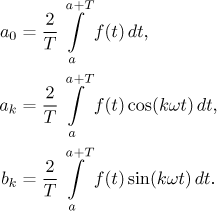
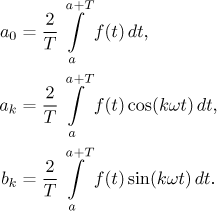
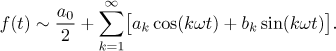
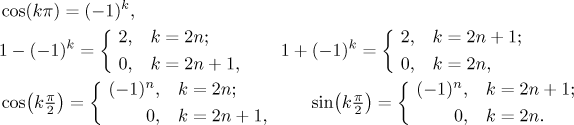
![]()