Problem: Expand the given function in a power (Taylor) series with the given center:
![]()
Solution:
Cosine hyperbolic is not a function whose series we would remember. Thus we
need to find some connection between this function and the quartet that we
do remember. After some soul searching the answer should be obvious: We can
write
![]()
Now we can use the
standard approach. The center 0 is
already fixed, so we simply expand the exponentials using the series for
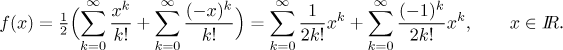
Note that the exponential expansion is valid for every x and
We have the answer expressed as a sum of two power series, but it is expected that we provide one power series. Thus the last step usually is to put the two series together if possible. Here it is actually very simple, note that both series feature the same powers of x and they have the same indexing. Thus we can write
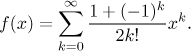
What are the values of the coefficients? For k odd we get 0, for k even we get 2 in the numerator. The series therefore in fact features only even powers and we can rewrite it accordingly, instead of k we will write 2k.
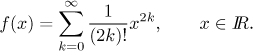
Note that this is almost exactly the same as the expansion for cosine, just
the alternating signs are missing. Would you make a guess how the expansion of