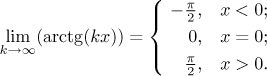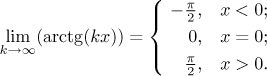Here we will show that having two sequences of functions,
{ fk} that converges to some
f on a set M and {gk}
that converges to some g on a set N (and assuming that all
gk map N into M), we cannot claim
that
{ fk(gk)}
converges to f (g), not even if the functions
involved are continuous.
Consider the functions
fk(x) = arctan(k⋅x),
we know that they form a convergent sequence and
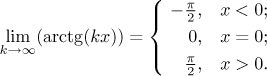
Denote this limit by f.
Consider also the functions
gk(x) = x/k,
it is easy to see that they converge to the constant function
g(x) = 0 on the whole real line.
What can we say about compositions?
For all k we have
fk(gk(x)) = arctan(x),
so
{ fk(gk)}
is a constant sequence of functions that converges to the function
arctan(x). On the other hand,
f (g) is the constant function
f (g(x)) = f (0) = 0, so
{ fk(gk)}
definitely does not converge to
f (g).