Vypouštění nádrže

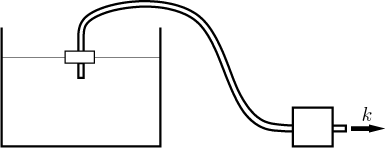
Zkusíme zde prozkoumat následující situaci: Máme nádrž naplněnou vodou a chceme ji vypustit. Jsou dvě přirozené kvantity, na které se můžeme zeptat: Kolik vody bylo z nádrže odčerpáno a kolik jí tam ještě zbývá. Budeme předpokládat, že vypouštění začalo v čase t = 0, a označíme jako V(t) objem vyčerpaný z nádrže do času t od počátku vypouštění; jako W(t) označíme objem, který v nádrži zbývá v čase t. Pro každý z příkladů vypouštění níže chceme určit tyto dvě funkce.

Všimněte si, že jestliže víme, kolik vody je na počátku, označme to V₀, pak nám znalost jedné z těchto funkcí automaticky dává znalost druhé, protože jsou spojeny vztahy

W(t) = V₀ − V(t),     V(t) = V₀ − W(t).

Obvykle se soustředíme na V, objem odčerpané vody, protože je přímo svázán s mechanismem vypouštění, takže se dají čekat jednodušší formulky. Navíc v případech, kdy neznáme V₀, je stejně v zásadě nemožné určit W, zatímco V dokážeme (ve většině případů) najít. Máme tedy důvody dávat obecně přednost V; za určitých podmínek může ovšem být W lepší, viz poslední příklad.

Je jasné, že odpověď (vzorce pro V a W) záleží na tom, jakým způsobem vypouštíme. Ukážeme tři různé způsoby vypouštění nádrže. První je vcelku triviální, ale ukážeme na něm několik zajímavých myšlenek. Druhý příklad je ten hlavní, kde přivedeme na scénu všechny důležité pojmy kalkulu. Třetí příklad vám asi přijde snadný, ale ve skutečnosti je z těch tří nejtěžší a nedokázali bychom jej zvládnout bez pojmů uvedených v druhém příkladě. Než začneme, ještě poznámku ohledně jednotek. V zásadě jsou irelevantní, jen se jich musíme držet po celé řešení. Pro jednoduchost jsme použili litry a minuty, ale klidně si místo nich dosaďte své oblíbence pro objem (galony, půllitry, lžičky, sudy, pinty atd.) a čas.

1. Pumpa s konstantním tahem

Zde si vezmeme hadici, jeden konec strčíme do pumpy a druhý do nádrže (na plováčku, chcete-li) a spustíme tu pumpu. Budeme předpokládat, že pumpa tahá vodu jistou konstantní rychlostí k litrů za minutu.

Tento typ příkladu se řeší na základce. Jestliže začneme vypouštět v čase 0, pak objem vypuštěný do jistého času t je

V(t) = k⋅t.

(Za předpokladu, že t není příliš velké. Po jistém čase - jmenovitě V₀/k - už žádná voda nezbyde a vzorec přestává platit, ale pak je situace triviální a nestojí za naši pozornost.)

A je to hotovo, naprosto triviální, že? Teď si s touto jednoduchou situací trochu pohrajeme, podíváme se na ni z různých stran, bude to všechno naprosto jasné, tak proč vlastně, no, chceme na tom ukázat různé koncepty a úhly pohledu, které se nám budou později hodit.

Za prvé, máme také obecnější vzorec. Objem vyčerpaný mezi časy t₁ a t₂ je

k⋅(t₂ − t₁).

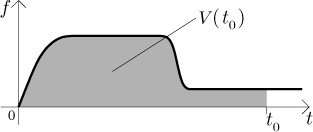
Za druhé, graf V vypadá takto:

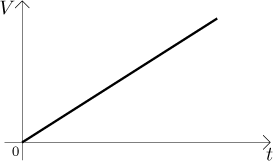
Kde se v tom obrázku schovává "čerpací konstanta" k? Je to směrnice této přímky. Jestliže nám někdo dá graf, jak bychom z něj to k dostali? To je elementární, je skryt v každém pravoúhlém trojúhelníku, který se nám zlíbí přilepit k této přímce tak, aby měl odvěsny rovnoběžné s osami.

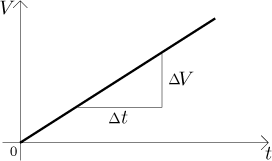
Když si vezmeme časový interval někde na ose x, označíme jeho velikost jako Δt, a jako ΔV si označíme odpovídající odtok vody z nádrže během tohoto intervalu, tak

Tato rovnice má několik zajímavých vlastností. Pokud budeme požadovat, aby platila pro všechny možné časové intervaly, pak už určuje růst V jednoznačně. Neurčuje ale jednoznačně funkci jako takovou, protože nejen ona V výše, ale i její posuny mají tento růst; jinými slovy, všechny funkce ve tvaru Z(t) = k⋅t + a splňují (1) pro všechny časové intervaly. Můžeme to tedy použít i pro jiné situace, když nezačínáme od nuly, ale nějaká voda už byla předtím vyčerpána.

V komplikovanějších situacích často nejsme schopni přímo dostat coby odpověď přesný vzorec (jako jsme to udělali před chvílí), ale obvykle dokážeme kýženou funkci alespoň popsat nějakou rovnicí. Rovnost (1) je dobrý kandidát, ale nestačí. Jak už jsme si všimli, definuje ne jednu, ale celou rodinu funkcí. Pokud chceme právě jednu, musíme přidat ještě další podmínku, a předchozí odstavec naznačuje jakou. Potřebujeme také specifikovat, co se dělo na začátku, tomu se říká počáteční podmínka. V našem případě začínáme od nuly. To už by mělo stačit; když řekneme, kde funkce začíná a jakým způsobem má odtud pokračovat, tak už nemá na výběr. Tím se dostáváme k modelu naší situace.

Funkce V(t) je jednoznačně dána následujícími dvěma podmínkami:
• V(0) = 0   a
• rovnice (1) platí pro všechny intervaly času Δt.

Takto tedy vypadá typický matematický model: Několik rovnic takových, že jestliže je nějaká funkce V splňuje, tak už popisuje naši situaci, a naopak ta pravá funkce splňuje ony rovnice. Jedna důležitá vlastnost modelu je jednoznačnost, což znamená, že jej splňuje jen jedna funkce - určitě by se nám nelíbilo, kdyby fyzika tvrdila, že když pustíme šutrák, tak buď spadne nebo poletí nahoru, podle toho, jak se zrovna cítí. Náš model ji má. Někdy není jednoznačnost možná už z podstaty studovaného jevu, například když upustíme balónek tak, aby jeho těžiště padalo přesně na hranu nože, nikdo pak nedokáže předpovědět, na kterou stranu se převáží.

Model, který jsme odvodili, má jednu zajímavou vlastnost: Jeho hlavní část, rovnice (1), je dosti univerzální. Neplatí jen na náš případ s pumpou fungující konstantním tahem. Jestliže pumpa všelijak blázní, pak se na chvíli uklidní, pak zase chvilku rošťačí, tak pořád rovnice (1) platí pro všechny časové intervaly, kdy zrovna pumpa táhne stejně. To se nám bude ještě hodit.

Zkusili jsme se podívat na naši jednoduchou situaci z obecnějšího pohledu a teď uděláme ještě jeden krok tímto směrem. Nechť funkce f (t) popisuje rychlost, jakou pumpa táhne vodu v čase t. V našem příkladě je tato funkce evidentně konstantní, f (t) = k pro všechna (relevantní) t. Jaký je vztah mezi V a grafem f ? Graf f je vodorovná přímka na úrovni k a výše odvozený vzorec říká, že hodnota V(t₀) je přesně obsah oblasti pod grafem f na intervalu ⟨0,t₀⟩.

Obecněji, voda odčerpaná mezi časy t₁ a t₂ je rovna obsahu oblasti pod grafem f nad intervalem ⟨t₁,t₂⟩.

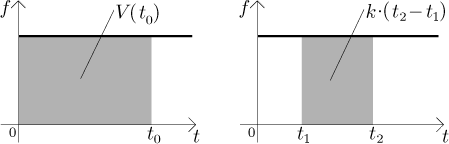
Všimněte si, že v tom druhém obecnějším případě tento fakt platí vždy, když je f konstantní na intervalu ⟨t₁,t₂⟩, její průběh jinde nehraje roli. To se ještě bude hodit.

Jak vidíte, z této jednoduché situace jsme toho dostali docela dost. Teď uvidíme, co se s těmito úvahami stane, když přejdeme ke komplikovanější situaci.

2. Pumpa s proměnným tahem

Opravdická pumpa nefunguje konstantně, protože její činnost ovlivňuje spousta faktorů, například proud, kterým je napájena, není vždy opravdu konstantní, samotný motor může jet nepravidelně atd. Dokonce můžete motor ovlivnit sami, například jej nastavit na pomalejší (a tudíž tišší) tah v noci nebo když vám ve dne spí děti. Rychlost, kterou je voda čerpána, proto není konstantní, ale závisí na čase; je tudíž možné ji popsat funkcí. Pro účely tohoto příkladu budeme předpokládat, že tato rychlost (budeme ji značit f ) je dána následujícím grafem, vybrali jsme něco jednoduchého.

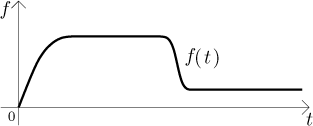
Jak se toto dá interpretovat? Na začátku jsme pumpu zapnuli, ale opravdická pumpa neskočí okamžitě na svůj plný výkon, dojde tam postupně. Poté pumpa jela (zdá se) konstantním tempem po nějakou dobu, dokud jsme nesnížili její tah (a zase změna nenastala okamžitě).

Tak už víme, jak pumpa jela, co se dá říct o funkci V popisující odčerpaný objem? Jedna věc je jasná, protože f není konstantní, nedokážeme rovnou dostat odpověď pomocí předchozího postupu. Existuje nějaký způsob, jak si pomoci alespoň trochu tím, co už známe?

Byl by tu jeden zajímavý nápad. Vezmeme nějaký čas t₀ a uvažujeme velice malinký časový úsek okolo tohoto konkrétního času. Protože f nevypadá příliš divoce, můžeme předpokládat, že když vezmeme opravdu velice malý časový úsek, tak se na něm f téměř nezmění, proto neuděláme velkou chybu, když budeme předpokládat, že je tam vlastně konstantní.

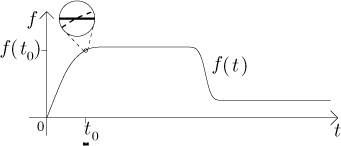
Pokud se soustředíme na ten konkrétní úsek, kde bereme f jako konstantu, tak můžeme aplikovat poznatky z předchozího příkladu (už jsme to tam diskutovali), například to, že V je (na tomto úseku) v zásadě přímka se směrnicí rovnou f (t₀). Vypůjčíme si nápad z prvního příkladu a budeme uvažovat nějaký trojúhelník přilehlý k této přímé části grafu V s vodorovnou odvěsnou délky Δt a odpovídající změnou objemu označenou ΔV.

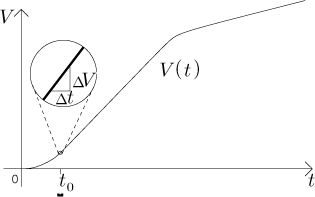
Zajímá nás jen ten malý kousek, takže tvar V jinde je irelevantní (což je dobře, protože ještě nevíme, jak V vypadá). Vypadalo by ale srandovně, kdybychom nakreslili jen malinký kousíček visící v prostoru, tak jsme zbytek V odhadli podle f: Nejprve se voda vypouští pomalu, ale pumpa se hned rozjede a objem pak narůstá rychle; pak pumpu zpomalíme a růst V se také příslušně zpomalí. Každopádně jak už jsme řekli, díváme se jen na ten malý kousek a z našeho odhadu, že na něm je graf V v zásadě přímka, dostaneme

Jak z této "téměř rovnosti" dostaneme něco přesného o V? Víme, že f je na našem úseku skoro ale ne zcela konstantní, takže tam děláme nějakou chybu. Odhadneme také, že se ta chyba zmenší, když zmenšíme časový úsek. Ona "téměř rovnost" se tak bude víc a víc blížit k rovnosti, když budeme brát menší a menší časové úseky symetrické okolo t₀. Teď je přirozené se zeptat, co by se stalo, kdybychom vzali nekonečně mnoho úseků, jejichž velikosti by se zmenšovaly k 0. Intuitivně by se dalo čekat, že pak chyba také půjde k nule a z "téměř rovnosti" se stane rovnost. Pokud ale chceme dostat nějaký spolehlivý závěr, pak musíme začít blíže zkoumat ten proces braní nekonečně mnoha zmenšujících se úseků a zjistit, jak se chová a co dělá - a zrodil se pojem limity.

Budeme předpokládat, že jsme ten nápad s uvažováním úseků s velikostmi jdoucími k nule ospravedlnili, a teď je otázka, co se stane v (téměř) rovnici nalevo. Abychom to uviděli, musíme nejprve zjistit, co ten zlomek vlevo znamená "v reálném světě". Uvažujme jeden takový podíl ΔV/Δt. Jaký má smysl? Objem vody přesunuté během jistého času děleno velikostí tohoto časového úseku. To známe, je to průměrná rychlost vypouštění vody. Jak necháme ty časové úseky smrskávat k t₀, tak se také ty trojúhelníky nutně zmenšují a děláme průměry přes menší a menší časové úseky, je tedy přirozené očekávat, že nakonec dostaneme pravou rychlost čerpání přesně v čase t₀.

Když tedy začneme s onou "téměř rovností" a provedeme smrskávací proces s úseky a trojúhelníky, dostaneme následující tvrzení: Rychlost, kterou se voda vypouští v čase t₀, je rovna rychlostí, kterou táhne pumpa. No tak to není zrovna objev století, ale je pěkné vědět, že naše úvahy vedly k něčemu, co je evidentně pravda, což naznačuje, že jsme se neodchýlili ze správné cesty.

Tím důležitým je zde způsob, kterým jsme k tomuto evidentnímu tvrzení přišli, protože nám to dává algoritmus k nalezení rychlosti změny V v čase t₀, jmenovitě pomocí aproximujících trojúhelníků. Umět nalézt rychlost změny nějaké kvantity je při zkoumání přírody zjevně užitečná věc, protože v přírodě se pořád všechno mění, a když chceme vědět, jaká pravidla za tím stojí, stává se znalost rychlosti změny zásadní. Vědci proto zkusili prozkoumat onen algoritmus zmenšujících se trojúhelníků teoreticky a v obecné situaci, doufaje v nalezení nějakých obecných odpovědí. To se jim povedlo a objevili jednoduchý algebraický způsob, jak z dané funkce rychlost změny dostat. Rozhodli se tuto rychlost změny nazvat derivace a používat značení V ′(t₀) pro rychlost změny funkce V v čase t₀. Můžeme tedy onen vztah "objevený" před chvílí zapsat jako V ′(t₀) = f (t₀).

Toto ukazuje, že matematika je především jazyk, zde jsme jej použili k přesnému zapsání "evidentního" pravidla o rychlostech změny. Jen když to zapíšeme přesně, pomocí matematického značení, můžeme doufat, že z toho dokážeme dostat nějakou informaci, například najít nějaký vzorec pro V.

Ona rovnost výše by měla platit v každém čase, takže je to podmínka, která nutí V růst určitým způsobem, určitou rychlostí. To ale ještě nepopisuje V jednoznačně. Musíme ještě říct, že na začátku nebylo nic vypuštěno. Tímto způsobem se dostáváme k modelu naší situace.

Funkce V popisuje, kolik vody bylo odčerpáno z nádrže, tehdy a jen tehdy, když tato funkce splňuje následující dvě podmínky:
• V ′(t) = f (t) pro všechna t,
• V(0) = 0.

Při zkoumání nějaké situace je obvykle vytvoření modelu prvním a nutným krokem na cestě k nalezení řešení. Pokus o zodpovězení otázky "co způsobuje, že se věci mění" se obvykle mění v následující otázku: "Které faktory ovlivňují rychlost změny?" Pojem derivace se tedy objevuje v zásadě všude a moderní věda by bez něj nebyla možná.

Poučení, část 1: Derivace je pojem, který se objevuje přirozeně v okamžiku, kdy si začneme klást dobré otázky o světě kolem (popravdě řečeno, matematici a fyzici se pořád ještě hádají o to, kdo s tím přišel dřív).

Teď se podíváme na hlavní otázku: Dokážeme vlastně najít tu funkci V určenou modelem, který jsme teď odvodili?

Zase použijeme myšlenku, že f je na malých úsecích v zásadě konstantní, ale teď to uděláme globálně. Začneme tím, že si pevně zvolíme určitou velikost úseku a pak rozdělíme časovou osu na po sobě jdoucí úseky této velikosti. Na každém úseku nahradíme f hodnotou této funkce uprostřed dotyčného úseku.

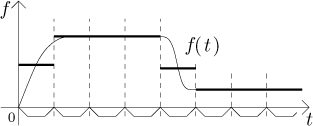
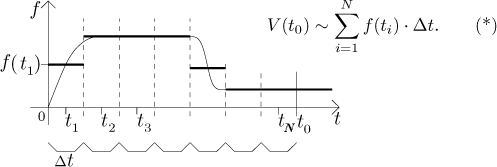
Teď vytvoříme funkci V*, která popisuje, kolik vody by se odčerpalo za předpokladu, že pumpu popisuje ona po částech konstantní funkce namísto skutečného f. Začneme prvním úsekem, a jestliže označíme jeho střed jako t₁, pak předpokládáme, že na tomto úseku pumpa táhne kostantní rychlostí f (t₁). Proto by na tomto prvním úseku měla být V* přímka se směrnicí danou onou konstantní rychlostí pumpování. Pak přejdeme na druhý úsek. Tam pumpa táhne stálou rychlostí (tentokráte danou hodnotou f v prostředním bodě t₂), takže tam graf V* musí být zase přímka, a protože objem vyčerpané vody nemůže náhle skočit, bude graf na druhém úseku spojen s grafem na prvním úseku. Pokračujeme tímto způsobem a dostaneme něco jako obrázek níže (zmenšili jsme měřítko na ose y, abychom dostali obrázek rozumné velikosti).

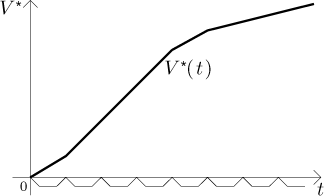
Jak věrná je tato aproximace grafu skutečné V? Porovnejme si, co se stalo na prvním úseku. Když jsme nahradili f její prostřední hodnotou, tak jsme rychlost vypouštění nejprve přehnali, ale na druhé polovině zase nedocenili, takže by se dalo argumentovat, že se to nějak vyruší a rozdíl nebude velký. To už ale neplatí o druhém úseku, kde jsme pořád přestřelovali, což ukazuje, že tento druh argumentu není moc užitečný. Lepší je jít na to takto: Připouštíme, že chyba aproximace může být velká, ale to je tím, že jsme vzali velké úseky. Pokud bychom vzali velice malé úseky, tak by byl rozdíl mezi f a použitými konstantami mnohem menší, proto by také výsledná V* byla lepším odhadem pro V.

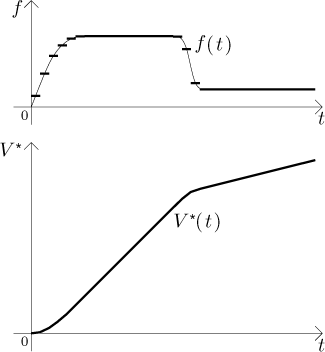
Je tu naděje, že kdybychom ten výpočet opakovali dokola se stále menšími a menšími velikostmi úseků, pak by se grafy příslušných funkcí V* měly blížit ke skutečnému grafu V. A opravdu, pokud není f příliš divoká (šílené oscilace nejde dobře aproximovat konstantami), pak je ten argument skutečně správný. Proces, který jsme právě popsali, je počátečním bodem pro dva směry dalšího zkoumání, praktický a teoretický.

Z praktického pohledu nám to nabízí realizovatelný způsob aproximování V(t₀) pro určité pevně zvolené t₀ pomocí vzorce, který lze snadno naprogramovat do počítače, takto: Částečný přínos pumpy, která tahá konstantní rychlostí k během časového úseku o délce Δt, je k⋅Δt. Když časový interval ⟨0,t₀⟩ rozdělíme na malé úseky, pro každý spočítáme příslušný částečný přínos a sečteme, tak dostaneme

Velice dobrou otázkou samozřejmě je, jak malé ty úseky mají být, když potřebujeme dostat odpověď s určitou přesností. Takovým problémům se věnuje celá jedna oblast matematiky.

Teoretický pohled na onu myšlenku schodové aproximace je následující. Můžeme zkusit teoreticky vykoumat, co se stane, když opakujeme tu proceduru nekonečně mnohokrát s úseky, jejichž velikosti se zmenšují k nule. Teorie říká, že když je f rozumně pěkná, tak se opravdu ty grafy V* blíží k V a také ten sčítací vzorec výše jde k jistému číslu A, které se rovná V(t₀). Navíc existuje relativně spolehlivý algebraický způsob, jak toto číslo A najít. Má nějaký význam? Začneme tím, že se vrátíme k aproximujícímu vzorci (*) pro V(t₀). V prvním příkladě jsme nabídli následující interpretaci: Toto číslo je rovno ploše oblasti pod po částech konstantní funkcí, která nahradila v našich výpočtech f, na intervalu ⟨0,t₀⟩.

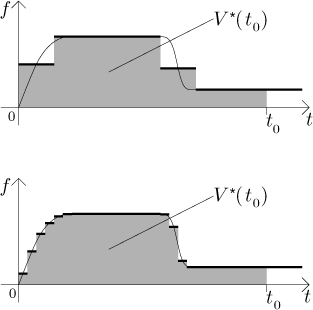
Když začneme dělat ty obdélníky užší a užší, pak se vzniklé po částech konstantní funkce blíží víc a víc k f, takže to číslo A, které nakonec dostaneme, je vlastně obsah oblasti pod grafem f na intervalu ⟨0,t₀⟩.

Tomuto číslu se říká určitý integrál funkce f od 0 do t₀ a máme pro něj speciální značení, takže náš výsledek můžeme přepsat jako

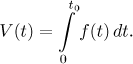
Připomeňme, že máme algebraický způsob, jak tento určitý integrál najít, který je pro pěkné funkce docela spolehlivý. Právě toto se studenti učí v kursech analýzy.

Poučení, část 2: Integrování je způsob, jak posčítat malé příspěvky přes určitý čas v případě, že nejsou konstantní, což je zase něco, co se vyskytuje často. Myšlenka integrálu se objevila přirozeným způsobem v době, kdy se rodily vědy. Můžeme tedy vinu hodit na fyziky, rozhodně neplatí, že matematici vymysleli integrál, aby mohli děsit studenty.

Zkusme shrnout, co jsme zatím udělali. Vytvořili jsme model naší situace, který byl založen na rovnici V ′ = f, a pak jsme ukázali způsob, jakým lze tuto rovnici vyřešit neboli najít funkci V, která jej splňuje. Hlavní rovnice obsahuje derivaci neznámé funkce, takové rovnice se jmenují diferenciální rovnice. Většina přírodních zákonů má tento tvar. Ta, kterou jsme zde řešili, je velice jednoduchá. Když se diferenciální rovnice trochu zesložití, tak se rychle ocitneme v situaci, kdy je určení řešení přesným výpočtem nemožné. Pak se uchýlíme k přibližným metodám a počítačům, vlastně se dá říci, že onen výše popsaný algoritmus s rozdělováním na úseky je základní metodou pro řešení diferenciálních rovnic.

Poznámka: Máme rovnici a máme vzorec pro její řešení. Co se stane, když je dáme dohromady?

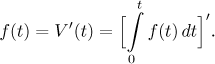
Vidíme, že když integrujeme a pak derivujeme, dostaneme se zpět, odkud jsme začali. Integrování a derivování jsou tak v jistém smyslu inverzní procesy (téměř ale ne zcela, více o tom zde v Math Tutoru hovoříme v sekci Základní věta kalkulu v části Integrály - Teorie - Úvod).

3. Díra v nádrži

Teď použijeme jiný, stejně přirozený způsob vyprázdnění nádrže, vyndáme špunt. Zase budeme chtít určit funkci V(t) popisující, kolik vody vyteklo za čas t.

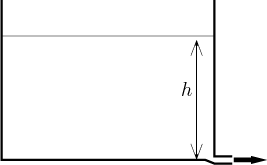
Jakou rychlostí plyne voda z díry? Nejprve budeme uvažovat velmi malinký interval času Δt, který je tak malý, že se důležité parametry v zásadě nemění. Můžeme si představit, že voda, která za tu dobu nádrž opustila, vytvořila válec, jehož základna je dána dírou a má určitý obsah, říkejme mu a. Výška tohoto válce je dána rychlostí vody v (můžeme předpokládat, že během tohoto velice krátkého intervalu je konstantní). Když náš interval začne, tak je nějaká částečka vody v díře (válec tam má svou bázi), a než ten interval skončí, tak tato konkrétní částečka urazí dráhu v⋅Δt a vytvoří vršek válce, takže toto číslo udává jeho výšku. Objem ΔV, který nádrž během tohoto času opustil nádrž, je tedy ΔV = a⋅v⋅Δt. Tato rovnice se dá napsat jako ΔV/Δt = a⋅v, takže když použijeme obvyklou fintu s uvažováním stále kratších a kratších intervalů, dostaneme následující vzorec pro rychlost změny V: V ′ = a⋅v.

Rychlost v závisí na tom, jak moc je voda vytlačována. Na základní škole nám řekli, že v tekutinách tlak nezávisí na celkovém objemu, ale jen na hloubce, tj. na výšce vodního sloupce nad naší dírou. Potřebujeme znát přesnou podobu této závislosti, takže se obrátíme na fyziku. Torricelliho zákon říká, že když je výška vodního sloupce nad dírou h, pak rychlost přímo závisí na druhé odmocnině z h. Když do toho započítáme průměr díry a další faktory (například gravitaci) a schováme je všechny do jedné konstanty, dostaneme vzorec pro rychlost změny V.

Abychom z toho dostali rozumnou rovnici, potřebujeme se nějak zbavit h. To znamená, že potřebujeme vědět víc o naší situaci. Asi nejjednodušší vztah mezi objemem a výškou vody nastává, když má nádrž stejný vodorovný průřez na všech úrovních (například když je to svislý válec nebo krychle). Pokud je plocha tohoto průřezu rovna A (a předpokládáme, že je střed díry na úrovni dna), pak máme vzorec W = A⋅h, kde W značí objem vody právě přítomné v nádrži.

Vyjádříme si h = W/A a dosadíme do naší rovnice, pak schováme konstantu A do k, vznikne z toho jiné k, ale pořád je to konstanta. Teď se ještě potřebujeme dostat od W k V, na to potřebujeme vědět, kolik vody tam původně bylo, označili jsme to V₀. Tak dostaneme následující rovnici:

Tato diferenciální rovnice spolu s počáteční podmínkou V(0) = 0 popisuje naši situaci. Je to vlastně složitější, než by to muselo být, dostaneme hezčí vzorečky, pokud se budeme soustředit ne na vodu vyteklou, ale na vodu zůstávající. Připomeňme, že W(t) značí objem vody, která v nádrži zůstala v čase t. Vzhledem ke vzájemnému vztahu mezi V a W je jasné, že rychlost, kterou V roste, je přesně opačná než rychlost, kterou se W zmenšuje (takže znaménko derivace je záporné) a naopak. Ona diferenciální rovnice a počáteční podmínka pak tedy zní

To mínus je logické, objem vody se zmenšuje, takže musí být derivace (rychlost změny) záporná. Odvodili jsme model, který jednoznačně popisuje, co se děje v nádrži.

Všimněte si, že se tato rovnice zásadně liší od té v druhém příkladě výše. Tam jsme už od počátku věděli, kolik vody odtéká v každém okamžiku, jen jsme potřebovali vymyslet nějký způsob, jak ty jednotlivé příspěvky sečíst. Zde je naprosto jiná situace. Jestliže chceme vědět, jak rychle proudí právě teď voda ven, musíme na to znát, kolik je tam teď vody, ale na to bychom potřebovali vědět, jakými rychlostmi voda proudila ven v předchozích časech, ale na to bychom potřebovali vědět, kolik vody tam v těch časech bylo, což nedokážeme zjistit, dokud nevíme, jak rychle odtékala ven, a tak dále až do zblbnutí, je to začarovaný kruh.

Pokud tedy chceme získat přesné řešení tohoto problému, potřebujeme na to pokročilejší metody. Popravdě řečeno je tento problém ve srovnání s jinými diferenciálními rovnicemi ještě dost jednoduchý, každý student kalkulu, který slyšel o separaci proměnných, by měl umět odvodit, že W je nutně dáno tímto vzorcem:

Jako obvykle tento vzorec funguje jen do té doby, než se nádrž vyprázdní, a snadno se spočítá, kdy k tomu dojde.

Už jsme poznamenali, že když jsou diferenciální rovnice příliš složité na to, aby šly řešit explicitně (určit řešení vzorcem, jak jsme to tu dělali), tak se obrátíme k přibližným řešením a počítačům. Jen tak ze zvědavosti, jak by to fungovalo tady?

Zvolili bychom si pevně nějakou opravdu malou velikost úseků času Δt. První úsek této velikosti začíná v počátku, můžeme předpokládat, že během tak krátkého času se objem a tudíž i výška vodního sloupce prakticky nemění. Proto je na tomto úseku rychlost výtoku v zásadě konstantní a je rovna k krát odmocnina z V₀ (viz diferenciální rovnice výše); když toto vynásobíme délkou našeho časového úseku Δt, dostaneme údaj o tom, kolik vody během tohoto krátkého úseku vyteklo. Když tento malý objem odečteme od původního objemu V₀, dostaneme číslo W₁, což je naše aproximace objemu zbývajícího na konci prvního úseku. To je také začátek druhého úseku.

Spočítáme novou rychlost změny objemu pomocí onoho vzorce výše a nového objemu W₁ a předpokládáme, že tak zůstane po celou dobu druhého úseku, čímž tam dostaneme konstantní výtok. Snadno tedy spočítáme, kolik vody vyteklo, a odečteme to od W₁, čímž dostaneme W₂ - náš nejlepší odhad pro objem vody zbylý na konci druhého úseku času, což je mimochodem čas t = 2⋅Δt. Přesné vzorce jsou

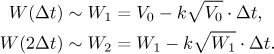
Pokračujeme tímto způsobem, cestou si značíme body W_k, které tvoří aproximace našeho W, a když je spojíme úsečkami, dostaneme graf, který je při troše štěstí blízký skutečnému grafu W. Proces skončí, když se s naším odhadem objemu dostaneme na (nebo pod) nulu. Opakovat takovéto výpočty je pro počítač hračka, a když si zvolíme opravdu malou velikost úseku, dostaneme dost dobrou aproximaci skutečného řešení daného tím vzorcem výše.

Poučení, část 3: Právě jsme ukázali, jak může analýza z prvního semestru pomoci při zpracování docela jednoduchých situací z reálného života, druhý a třetí příklad by bez ní nešly vyřešit.

Obecná poznámka o modelech

Matematický výsledek, který z modelu nakonec vyleze, se s reálnou situací shoduje jen tak dobře, jak dobře ji popisuje ten model. Platí to i o našich příkladech. U prvních dvou příkladů jsme měli nevyslovený předpoklad, že voda vytékající z nádrže je přesně ta voda protékající pumpou. Pokud se tedy naše situace liší - nádrž někde netěsní, pumpa není v pořádku, hadice má dírku - a tento rozdíl není zanedbatelný, pak teoretické vzorce pro V nebudou fungovat.

Podobně ve třetím příkladu předpokládáme, že ta naše díra je jediná, že tvar je pravidelný podle stanovených požadavků, a také předpokládáme, že střed díry je na úrovni se dnem nádrže. Torricelliho zákon totiž jako h bere vzdálenost mezi hladinou v daném okamžiku a středem otvoru. Pokud je tedy díra na jiném místě (když ji třeba uděláme trochu nade dnem), pak se změní vzorec pro h a dostaneme jinou rovnici a také jiné řešení.

Vytváření správného modelu tedy prochází několika etapami. Nejprve najdeme všechny faktory, které námi studovaný proces ovlivňují. Pak se snažíme zachytit v rovnicích, jak tyto faktory fungují. V dalším kroku zkusíme tento model vyřešit, tedy hledáme funkci(e) tento model splňující. V případě, že to není možné (což je často), používáme rozličné numerické metody k získání přibližného řešení. Pak se musíme zeptat, jak dobře se toto řešení shoduje se skutečnou situací, kterou studujeme, zejména jak dobře ji popisuje náš model. V této fázi pomůže udělat skutečný experiment (vypustit nějakou konkrétní nádrž) a porovnat naměřené hodnoty s těmi spočítanými naším postupem. Pokud se shodují, tak to ještě nic neznamená (mohla to být náhoda), ale naznačí to, že to nemusí být úplně špatně. Pokud se liší, začne se hledat, jaký podstatný vliv v našem modelu chybí.

Další příklad
Zpět na Proč?