Dělení polynomů a trik "přičtu-odečtu"

Dělení polynomů se zbytkem je jeden ze základních algebraických postupů a zde v analýze se používá zejména při rozkladu na parciální zlomky. Tento algoritmus předvedeme na vhodném příkladě.

Příklad: Vydělíme se zbytkem

• Nejprve vydělíme člen s nejvyšší mocninou dělence (čitatel zlomku) členem s nejvyšší mocninou dělitele (jmenovatel zlomku). V našem případě dostaneme 2x³ : x² = 2x. Máme tedy první člen podílu:

  

• Tímto členem podílu vynásobíme dělitel a odečteme od dělence:

  

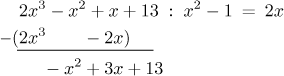
• Má-li zbytek menší stupeň než dělitel, výpočet je hotov. V opačném případě se vrátíme zase na začátek a dělíme nejvyšší člen zbytku nejvyšším členem dělitele atd.

V našem příkladě obrdržíme

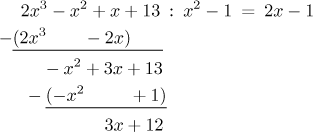
a tedy

Trik "přičtu-odečtu"

Jde o velmi obecný trik, který se občas používá při práci s algebraickými výrazy. Často jsme v situaci, kdy bychom opravdu ocenili, kdyby v daném výrazu něco určitého bylo, ale není to tam. V mnoha případech si to tam dokážeme přidat přičtením, ale pak to musíme vybalancovat tak, že dotyčnou věc zase odečteme.

Ukážeme si aplikaci na příkladě výše, tentokráte zkusíme vydělit jinak. Například by se nám velice líbilo, kdyby v čitateli bylo 2x³ − 2x, tak si to tam vyrobíme a pak toho využijeme.

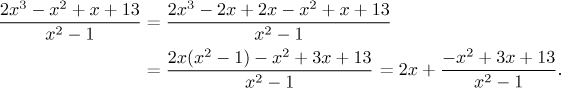
Teď by se nám velice líbilo, kdyby v čitateli bylo -x² + 1, tak si to tam zase vyrobíme.

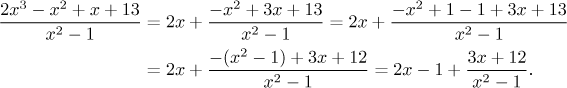
Tento způsob dělení může být někdy opravdu rychlý a pohodlný.

Existuje podobný trik, který můžeme nazvat "vynásobím-vydělím". Představte si například, že máme výraz 3x + 5, ale raději bychom u x měli koeficient 7 a také tam nechceme žádné další členy s x. Ten poslední požadavek vylučuje přičtení a odečtení, ale můžeme udělat toto:

3x + 5 = 3⋅(x + 5/3) = (3/7)⋅(7x + 35/3).