Funkce více proměnných: Integrál

Začneme sice formálně nesprávnou, přesto výstižnou představou určitého integrálu pro funkci jedné proměnné. Výraz

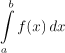
je definován jako "obsah pod grafem", my si můžeme myslet, že jakoby "sčítáme" hodnoty funkce v bodech x, ale sčítáme je ve formě obsahů teňounkých sloupečků, obdélníčků. V každém bodě x je obdélníček o výšce f (x) a šířce dx, kde dx je chápáno jako nekonečně malý kousek osy x, je to diferenciál délky. Obsah takového obdélníka je pak f (x)⋅dx a sčítáme je symbolem ∫.

Z toho vychází představa pro funkce více proměnných. Máme-li nějakou množinu Ω v ℝⁿ a na ní funkci f, pak také můžeme "sčítat" hodnoty. Tentokráte ale nesčítáme ploché obdélníčky, ale vícedimenzionální "sloupy". Pokud je Ω v ℝ², tedy máme funkci dvou proměnných, tak si nad každým bodem můžeme představit teňounký váleček o výšce f () a základně dA, kde dA je tentokráte nekonečně malý kousek roviny, je to diferenciál plochy.

Když "posčítáme" pomocí symbolického operátoru ∫ jejich objemy, které jsou zjevně f ()⋅dA, dostáváme

Tomuto říkáme dvojný integrál. Jeho význam je intuitivně jasný, je to objem objektu se základnou Ω a horní stranou danou grafem funkce f. Podobně jako u jedné proměnné, i zde objemy odčítáme pro body, kde f () < 0, je to tedy "matematický objem". Poznamenejme, že důležitá je představa sloupečků, nemusí to být nutně přímo válečky. Například později pro nás bude užitečné pracovat se sloupečky o čtvercové základně.

Myšlenku dvojného integrálu pak hravě zobecníme na funkce více proměnných, třeba

je čtyřrozměrná velikost objektu "pod" grafem funkce f tří proměnných. Protože taková f má proměnné z prostoru ℝ³, jsou "základny" sčítaných "sloupečků" třírozměrné, odtud označení dV, je to diferenciál objemu. Říká se tomu trojný integrál, obecně mluvíme o vícerozměrných integrálech. Evidentně není snadné představit si řekněme sedmirozměrný sloupeček se šestirozměrnou základnou, ale to by neměl být problém, protože základní myšlenka je stále stejná. My prostě "sčítáme" hodnoty funkce ve všech bodech ze zadané množiny Ω.

Poznámka.
Něco o terminologii: V matematické analýze je slovo "oblast" speciálním termínem pro množiny, které jsou souvislé a otevřené. Bohužel, u vícenásobných integrálů se stejné slovo tradičně používá pro množinu, přes kterou integrujeme, bez ohledu na její vlastnosti. Je pravda, že obvykle integrujeme přes souvislé množiny, ale jen zřídka jsou otevřené, dokonce je to tak, že Ω jsou ve většině případů uzavřené. To je nemilé, ale slovo "oblast" se k integrování jaksi hodí a skoro každý to používá. Aby byl tento text přesný, snažil jsem se psát důsledně "množina", ale stejně mi sem začaly oblasti nějak lézt, tak jsem to tak nechal. Vemte tedy prosím na vědomí, že v této kapitole oblast neznamená klasickou matematickou oblast, například nemusí být otevřená, je to jen jiné slovo pro množinu.

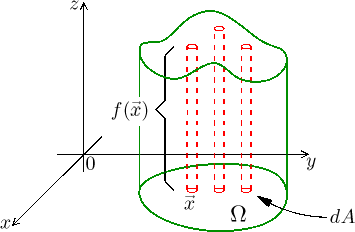
Hlavní myšlenka vícerozměrného integrálu je jasná, není ovšem zřejmé, jak by se takový integrál počítal v praxi. Vyzkoušíme oblíbený nápad a budeme pracovat s řezy, čímž se problém převede na jednorozměrné integrování. K řezům ve směru os se dostaneme tak, že si "sloupečky" chytře zorganizujeme.

Jako obvykle se nejprve pořádně podíváme na funkce dvou proměnných. Tam se nám bude hodit představa, že sčítáme supertenké hranolky, jejichž základny dA jsou nekonečně malé čtverečky dx×dy. Zvolíme si základní směr, řekněme směr osy y. Jako u derivací si pevně zvolíme jisté x = x₀ a podíváme se na všechny hranolky, které odpovídají této hodnotě. Stojí těsně vedle sebe, mají shodnou šířku dx a vytvářejí proto jakousi desku s vykousaným horním okrajem (ten je daný funkcí f ). Objem této desky získáme, když její boční plochu vynásobíme tloušťkou dx.

Ona boční plocha, jinak viděno řez grafem funkce f, se najde snadno, je to vlastně plocha pod grafem funkce y ↦  f (x₀, y), tedy klasický integrál funkce jedné proměnné.

Zkusme to zformulovat přesněji. Pokud si zvolíme x = x₀, zajímá nás množina všech bodů (x₀, y), které leží v dané množině Ω. Jinak řečeno, bavíme se tu o přímce vedoucí definičním oborem ve směru osy y, podobně jako v předchozích kapitolách, a nás zajímá její průnik s množinou Ω. Tento průnik může být i velmi divoký, ale my se zde pro jednoduchost omezíme na takové tvary Ω, pro které budou všechny takovéto řezy (pro všechny volby x) buď prázdné (ty nás nezajímají), nebo budou mít podobu úsečky s jistými okraji c(x) a d(x).

Pro zvolené x₀ nás tedy budou zajímat body (x₀, y) pro hodnoty y splňující c(x₀) ≤ y ≤ d(x₀). Pro tato y máme funkci (o jedné proměnné) y ↦  f (x₀, y), kterou při troše štěstí budeme umět integrovat. Výpočtem získáme číslo

což je dvourozměrný obsah řezu tělesa pod grafem funkce f.

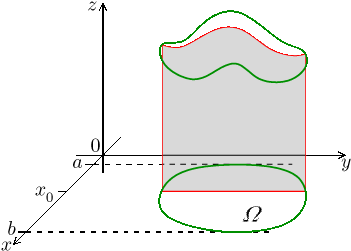
Z praktického pohledu předstíráme, že x je konstanta, a integrujeme podle y. Je to obdobný proces jako u parciálního derivování, takže by to nemělo činit problémy. Všimněte si, že dostaneme číslo, které záleží na volbě x, ale proměnná y se již ztratí při integrování.

Když tuto hodnotu vynásobíme "tloušťkou" dx, získáme číslo

což je objem řezu coby trojrozměrného objektu, jak jsme si jej vytvořili zorganizováním určitých hranolků.

Další řezy dostáváme měněním oné zafixované hodnoty x. Abychom dostali celý hledaný objem, musíme "sečíst" objemy jednotlivých řezů, což se zjevně stane integrováním pomocí x. Vše do sebe krásně zapadá, protože jsme si již rozmysleli, že hodnoty objemů řezů záleží právě na volbě x. Nejmenší hodnota a a největší hodnota b pro x jsou dány tím, které řezy množinou Ω jsou neprázdné. Dostáváme vzorec

Aby toto fungovalo, musí být Ω tak tvarovaná, aby se daly rozumně určit funkce c(x), d(x) pro okraje řezů a meze a, b pro x. Jinými slovy, mluvíme o oblastech Ω mezi dvěma křivkami nad intervalem:

Ω = {(x, y)∈ℝ²;   a ≤ x ≤ b   a   c(x) ≤ y ≤ d(x)   pro všechna   x∈I}.

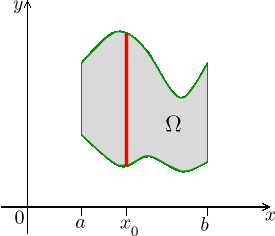
Pak

Takovému přepisu dvojného integrálu říkáme dvojnásobný integrál.

Je dobré naučit se pracovat jen s obrázkem oblasti Ω, bez odvolávání na graf funkce (který potřebuje o dimenzi víc). My chceme dvojným integrálem projít všechny body množiny Ω. Rozhodli jsme se brát to po úsečkách rovnoběžných s osou y, v našem obrázku po svislých řezech. Vnitřní integrál jede po typickém řezu, jehož konce samozřejmě závisí na konkrétní poloze tohoto řezu, tedy na hodnotě x. Vnějším integrálem pak změnami x procházíme jednotlivými řezy.

Samozřejmě není důvod začínat řezy ve směru y. Množina Ω může být orientována naopak,

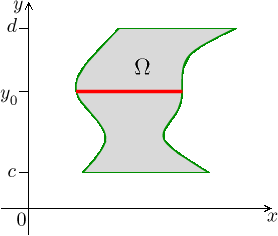
neboli jde o množinu ve tvaru

Ω = {(x, y)∈ℝ²;   c ≤ y ≤ d   a   a(y) ≤ x ≤ b(y)   pro všechna   x∈I}.

Pak je možné řezat ve směru osy x. Přes typický řez integrujeme pomocí x (pohyb zleva doprava), meze závisí na poloze řezu dané volbou y. Výsledná čísla pak "sečteme" dalším integrálem, tentokráte vzhledem k y.

Toto je tedy druhý možný převod dvojného integrálu na integrál dvojitý.

Některé množiny vyhovují oběma specifikacím, pak máme na výběr, kterým směrem budeme řezat.

Příklad.
Budeme integrovat funkci f (x, y) = y⋅e^x přes 2D interval ⟨0,1⟩×⟨1,3⟩ neboli množinu

Ω = {(x, y)∈ℝ²;   0 ≤ x ≤ 1   a   1 ≤ y ≤ 3}.

Máme na výběr, pomocí které proměnné integrovat nejdříve, protože v obdélníku budou obojí směry řezů fungovat. Pokud budeme chtít nejprve integrovat s y, tedy zafixovat x a řezat ve směru osy y, tak se y mění mezi 1 a 3 bez ohledu na polohu řezu.

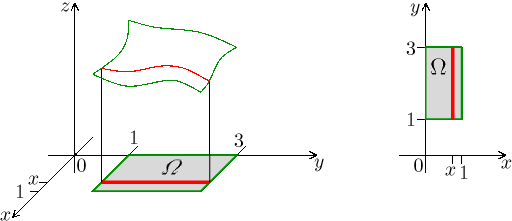
Obrázek vlevo je ryze symbolický, graf dané funkce nejspíš vypadá jinak, je jen pro připomenutí situace, nás zajímá spíš obrázek vpravo. Z něj bychom měli vyčíst vše potřebné pro sestavení integrálu.

Pro integrál přes jeden řez dostáváme

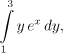
kdy bereme x jako konstantu. Pak je i e^x konstanta a máme

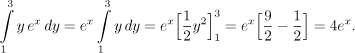
Přesně podle očekávání se proměnná y vytratila a "obsah" řezu již závisí pouze na jeho pozici dané hodnotou proměnné x. Tyto řezy (integrály) pak "posčítáme" pomocí x, dostáváme

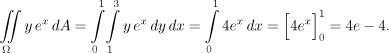
Některá poučení:

1) Ne vždy je možné nepoužívanou proměnnou úplně vytknout. Neměl by to být problém, stačí si pořád představovat, že jisté členy jsou konstantní, a pracovat s nimi jako obvykle. První integrál se tedy dal počítat i jako

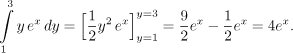
Protože ve funkci jsou dvě proměnné, raději jsme si v dosazovací fázi připomněli, za co máme meze dosadit.

2) Nemusíme řezy počítat zvlášť, lze nejprve sestavit celý integrál a pak jej spočítat. Vždy se ale postupuje tak, že se nejprve integruje integrál vevnitř a pak ten vně, pak případně další ještě více vně a tak dále. Meze a diferenciály k sobě patří vnořeným způsobem, integrál vně patří k diferenciálu vně, integrál druhý od kraje patří k druhému diferenciálu od kraje atd. Není možné to míchat. Protože při výpočtu znovu a znovu integrujeme, takovýmto integrálům se také říká "opakované integrály".

3) Je možné začít integrál sestavovat zvenčí. To si ukážeme u dalšího příkladu níže.

Jako opakování sestavování integrálu zevnitř (tedy od řezů) si vyzkoušíme vodorovné řezy, které jsou také možné.

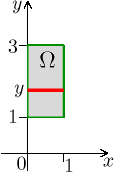
Z obrázku vyčteme, že na řezu se proměnná x vždy pohybuje mezi 0 a 1, dostáváme

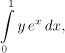
kde bereme y jako kostantu. Tyto integrály pak "posčítáme" pomocí y, vychází

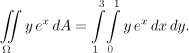
Říkáme, že jsme k zadanému dvojnému integrálu sestavili odpovídající dvojnásobný integrál k výpočtu. Počítáme zevnitř, což z cvičných důvodů zvýrazníme přepsáním integrálu se závorkou, což se normálně nedělá.

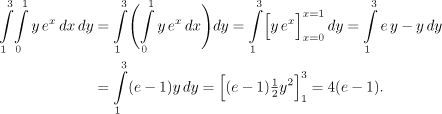
Při dosazování do vnitřního integrálu jsme si pro jistotu připomněli, která proměnná byla v té chvíli pracovní, tedy za kterou máme dosazovat.

Shrneme si to. Když máme dvojný integrál

přepíšeme si jej jako dvojnásobný integrál

(popřípadě v opačném pořadí). Při výpočtu pak začneme tím, že počítáme tzv. vnitřní integrál

čímž vznikne funkce proměnné x. Pak následuje vyhodnocení tzv. vnějšího integrálu

Porovnejme oba způsoby přepisu v příkladě výše:

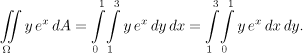
Vypadá to, že jsme prostě jen prohodili pořadí integrálů a odpovídajících diferenciálů "d". Takto snadno to ovšem funguje pouze u integrace přes obdélníky. Jinak je tzv. "záměna pořadí integrace" poněkud složitější.

Příklad.
Budeme integrovat funkci f (x, y) = e ^x2 přes konečnou oblast Ω vymezenou křivkami y = 2x, x = 1 a y = 0. Tentokráte ukážeme, jak sestavit opakovaný integrál zvenčí.

Vždy se vyplatí nakreslit obrázek integrační oblasti, je to trojúhelník s vrcholy (0,0), (1,0) a (1,2). Svislé řezy (ve směru osy y) budou určitě fungovat.

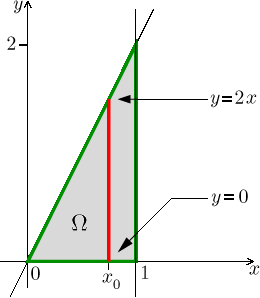
Vidíme, že pro určení polohy řezu má smysl volit x jen z rozmezí 0 až 1, čímž je dán vnější integrál, výsledný dvojnásobný integrál tedy bude mít tvar

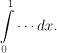
Na jednom konkrétním řezu se pak proměnná y pohybuje mezi hodnotami y = 0 a y = 2x. To ostatně odpovídá formálnímu přepisu množiny ve tvaru

Ω = {(x, y)∈ℝ²;   0 ≤ x ≤ 1   a   1 ≤ y ≤ 2x}.

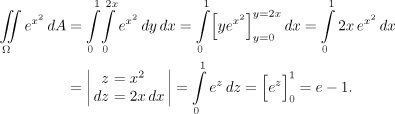
Nyní vyzkoušíme řezy ve vodorovném směru.

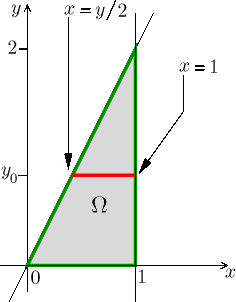
Poloha řezu je dána volbou y v rozmezí 0 až 2, tím je jasný vnější integrál. Řez (na kterém je pracovní proměnná x) je úsečka s pravým koncem na úrovni x = 1, levý konec leží na křivce y = 2x a nás zajímá, kolik je tam x. Vidíme tedy, že při pohybu podél takového řezu se x mění od y/2 po 1. Dostáváme

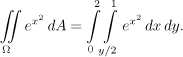
Začneme vnitřním integrálem

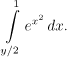
A hned máme problém, primitivní funkci k e ^x2 nelze vyjádřit elementárním algebraickým vzorcem, takže jsme skončili.

Vidíme, že někdy volba směru řezu neboli volba pořadí při integrování může mít vliv na to, jak to dopadne. V méně extrémním případě může ovlivnit složitost výpočtu.

Ačkoliv jeden výpočet nevyšel, přesto to bylo užitečné cvičení. Oba dva přepisy do dvojnásobného integrálu byly zcela v pořádku a umět takto integrál rozepsat je základní znalost. Viděli jsme také, že se při změně pořadí integrace meze nezachovaly.

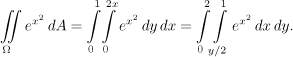
To je typické, při změně pořadí se musí meze znovu přepočítat. Někdy se potkáme s úlohou, že je nám zadán dvojnásobný integrál a máme změnit pořadí integrace (například proto, že v daném pořadí nelze najít primitivní funkci). V takovém případě je třeba nejdříve z tvaru mezí odvodit, jak vlastně vypadá integrační oblast Ω (jakýsi "reverse engineering"), a na ní pak aplikovat řezy druhým směrem.

Onen dvojí rozpis integrálu výše ukazuje ještě jednu věc, kterou si zejména začátečníci musí hlídat. Správně sestavený dvojnásobný integrál mimo jiné splňuje následující: Vnější integrál má jako meze pouze čísla. Vnitřní integrál může mít jako meze čísla nebo výrazy proměnnou, v tom případě to ale musí být ta proměnná, která je vnější, tedy v seznamu diferenciálů až na konci.

Zvídavého čtenáře jistě napadlo, že ne všechny oblasti Ω spadají do dvou probraných typů. V takovém případě obvykle není problém dotyčnou oblast rozdělit na podoblasti, které jsou již vhodného typu, a každou z nich rozkládáme zvlášť. Toto je možné díky linearitě integrálu vůči integrační oblasti. Přesné vyjádření je ve více dimenzích poněkud složité, ale nepřesně vyjádřeno by to fungovalo takto:

Uvažujem oblast Ω, kterou si rozdělíme na podoblasti Ω₁,...,Ω_m v následujícím smyslu: Ω = Ω₁∪⋅⋅⋅∪ Ω_m a podoblasti Ω_i se navzájem pronikají nejvýše na svých hranicích, či jinak řečeno, vzájemné průniky těchto podoblastí mají nulovou plochu. Pak

Příklad.
Nechť Ω je oblast mezi y = x² + 1 a osou x na ⟨0,1⟩. Chceme najít

Nejprve si nakreslíme Ω a rozmyslíme si obě možnosti pro řezy.

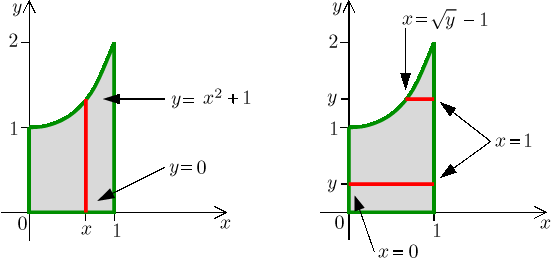
Tvar oblasti přímo vyzývá ke svislým řezům, kdy nejprve integrujeme podle y. Vidíme totiž, že pokud bychom se pokusili o řezy ve směru x, tak bychom neměli jednotné zadání pro levé konce řezů.

Takže vnitřní integrál bude používat proměnnou y. Rozmyslíme si, že pokud integrujeme funkci 8x(x² − y + 1)³ podle y, tak je 8x vlastně konstanta a dá se z integrálu vytknout. Při integrování výrazu (x² − y + 1)³ podle y je i x² + 1 jakoby konstanta, čili vlastně integrujeme výraz ve tvaru (−y + a)³. Zkušení integrátoři to zvládnou zpaměti, ti opatrní či méně zkušení si pomohou substitucí. Při její přípravě je klíčové derivovat podle té správné proměnné---je to samozřejmě ta, se kterou právě integrujeme.

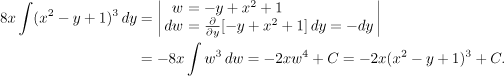
Dostáváme

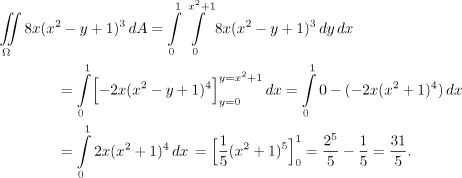
Co kdybychom z nějakého důvodu mermomocí chtěli řezat ve směru x? Zatímco pravý konec řezů se stále řídí stejným předpisem x = 1, levé konce mají jeden předpis x = 0 pro y∈⟨0,1⟩ a jiný předpis pro y∈⟨1,2⟩, tam x začíná na křivce y = x² + 1, tedy x má začáteční hodnotu . Tento problém se hravě vyřeší tím, že si oblast Ω rozdělíme na horní a dolní část, každá z nich je správného tvaru. Jinak řečeno, sestavíme dva integrály.

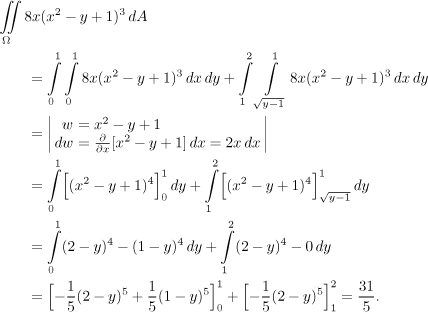
Uf, vyšlo to stejně, celou dobu jsem trnul, jestli nebudu muset hledat chybu ve výpočtu.

A to je v zásadě všechno.

Poznámka.
Pokud vás zajímá, jak se dělá trojný integrál

V tomto případě je Ω třírozměrný objekt. Potřebujeme sečíst hodnoty f ve všech bodech této množiny, k tomu si je potřebujeme vhodně zorganizovat pomocí řezů.

Pokud si zafixujeme jednu proměnnou, třeba x, získáme tím řezy tímto tělesem, které jsou kolmé na osu x, ovšem jen pro hodnoty x z jistého rozmezí a až b. Dostáváme tak první patro rozkladu

Teď je třeba integrovat přes typický řez, což je ovšem dvojrozměrný objekt ve směrech y a z, jehož přesný tvar závisí na volbě x. Pokud máme štěstí, půjde o objekt rozumného tvaru, přesně řečeno jednoho z těch základních dvou, které jsme probrali výše.

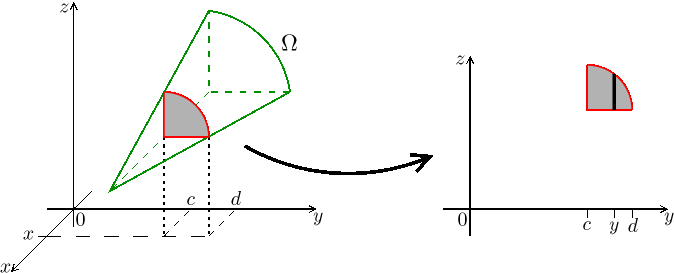
Dvourozměrné integrály už umíme, při troše štěstí například budou fungovat (přímkové) řezy ve směru y. Ty mají smysl jen pro y mezi jistými hodnotami c(x) a d(x), protože tvar dvojrozměrného řezu závisí na x, a pak už proměnnou z běháme po úsečce, jejíž konce závisí jak na konkrétním dvojrozměrném řezu neboli na x, tak na volbě úsečky neboli na y. Dostáváme tak

Samozřejmě v závislosti na tvaru Ω nevíme, zda zrovna toto pořadí řezů bude fungovat, je celkem šest možností, alespoň jedna by mohla zabrat.

Je zjevné, že pro zdárné sestavení takového integrálu je třeba umět se dobře orientovat v prostoru a mít zvládnutou analytickou práci s geometrickými útvary.

Poznámka.
K čemu by mohlo být takové "sčítání hodnot"? Ukážeme jeden příklad.

Když máme n čísel x₁,x₂,...,x_n, najdeme jejich průměr pomocí vzorce

potřebujeme je na to sečíst.

Pokud máme funkci f na nějakém intervalu ⟨a,b⟩, najdeme její průměrnou hodnotu na tom intervalu vzorcem

Pokud máme funkci f (x, y) na oblasti Ω, najdeme její průměr na této množině vzorcem

A pokud máte funkci T(x, y,z) popisujícím teplotu v rozličných místech jisté místnosti, tak k určení průměrné teploty v místnosti budete muset "sečíst" všechny hodnoty T pomocí trojného integrálu T přes dotyčnou místnost (a pak vydělit jejím objemem).

Zpět na Extra - Funkce více proměnných