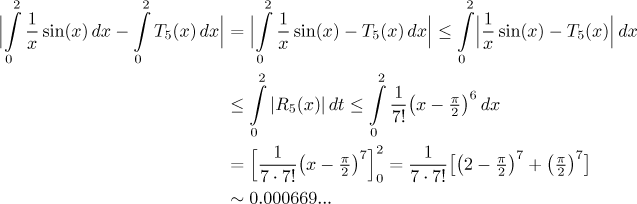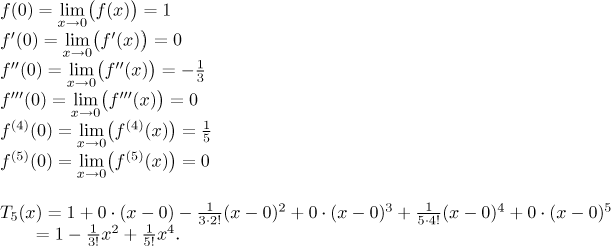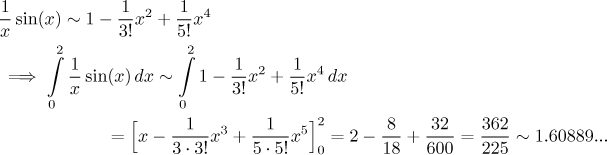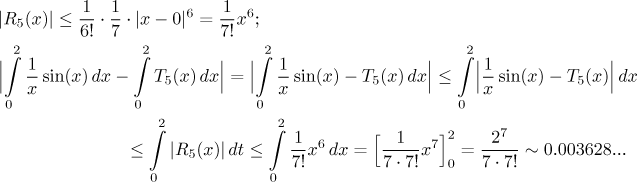27: The derivative

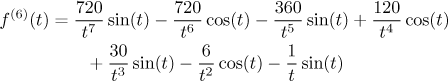
is so terrible that straightforward methods (find its derivative f ⁽⁷⁾, check on critical points etc) do not work here. One has to get rather devious, see here, to find that f ⁽⁶⁾ is in fact increasing on [0,2] and thus
      max = f ⁽⁶⁾(2) = −19sin(2)/8 − 21cos(2)/4 = 0.02518950...,
      min = lim ₀ ( f ⁽⁶⁾) = −1/7.
When taken in the absolute value, the maximu is given by the larger (in absolute value) of the two, which is 1/7. Thus

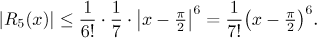
Now we use it in estimating the error of integration.

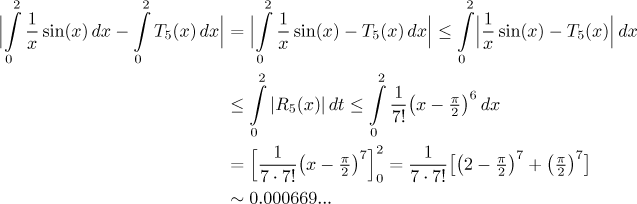
Alternative: The calculations for Taylor's polynomial yield

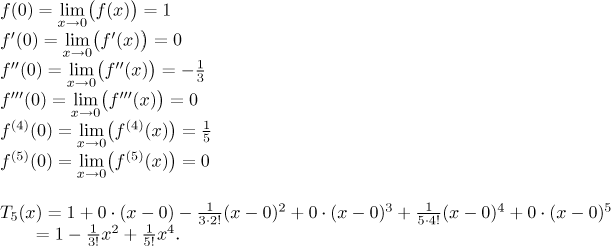
Note that remarkably, this is exactly what one gets when finding the T₆ for sin(x) and then dividing it by x.

Then one gets

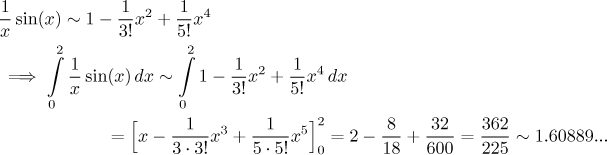
The error estimate needs the same maximum, so we get

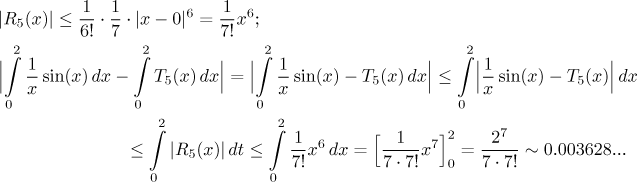
The error estimate is worse, which is to be expected. The center a = 0 is at one end of the integrating interval, so at the other end the approximation is no longer as good, while the centre a = π/2 is closer to the centre of this interval. Still, from practical point of view this alternative approach is better, since the Taylor polynomial that we get is simple to extend further, we easily improve precision by taking for instance T₇, while for the centre a = π/2 raising the degree would mean more really ugly derivatives.

Answer
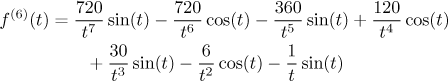