Zde se podíváme na nejdůležitější příklady posloupností. Soustředíme se na jejich konvergenci, zmíníme se také o omezenosti a monotonii posloupností, které tady uvidíme poprvé. Po alternující a aritmetické posloupnosti se podíváme na geometrickou posloupnost, pak se podíváme na mocniny, faktoriál, exponenciálu a nakonec na sinus a kosinus.
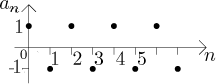
Jak už jsme viděli, prototyp
alternující posloupnosti

Už z obrázku vidíme, že tato posloupnost nemá limitu. Toto je nejjednodušší příklad problému typu oscilace zabraňujícího existenci limity.
Chování aritmetické posloupnosti
Jestliže
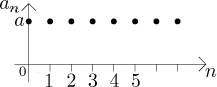
Z obrázku se zdá jasné, že tato posloupnost konverguje, a opravdu platí, že
![]()
Jestliže
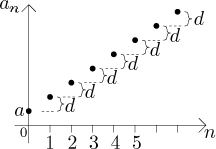
Taková posloupnost je divergentní, ale limita existuje a je rovna nekonečnu;
to jest,
Jestliže
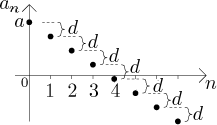
Taková posloupnost je zase divergentní, ale má limitu, tentokráte mínus
nekonečno; tedy
Chování geometrické posloupnosti
Pro další případy je dobré si připomenout čtyři typické příklady, které jsme
viděli v části Teorie
- Úvod - Důležité příklady. Reprezentovaly čtyři alternativy, které se
mohou stát pro
Případ 1:
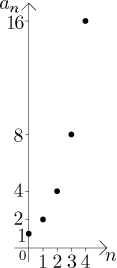
V tomto případě posloupnost diverguje, ale má limitu, jmenovitě nekonečno (viz konec poznámky zde).
Případ 2:

a když
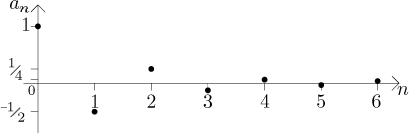
z pohledu konvergence je to tentýž případ: posloupnost konverguje k 0.
Případ 3:
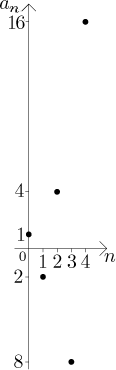
V tomto případě posloupnost nemá limitu. Všimněte si, že tento příklad kombinuje oba důvody divergence diskutované v úvodu k limitě: oscilaci a "vybouchnutí".
Fakta o geometrické posloupnosti lze shrnout několika způsoby. Z pohledu konvergence (a s vynecháním některých alternativ) máme pěkné a užitečné tvrzení:
Fakt.
Geometrická posloupnost{qn} diverguje, jestliže|q| > 1, a konverguje k 0 pro|q| < 1.
Je také možné vyjádřit všechny detaily:
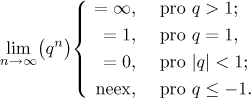
Ačkoliv je
Případ 1: (mocnina v čitateli). Posloupnost
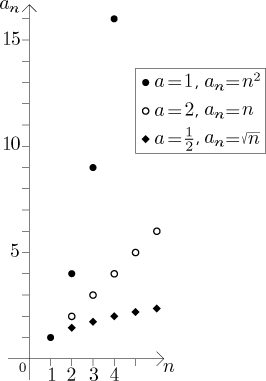
Máme následující fakt:
![]()
Případ 2: (mocnina ve jmenovateli). Posloupnost
![]() , kde
, kde
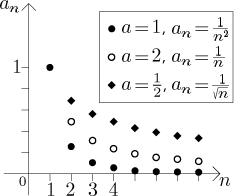
Máme následující fakt:
![]()
Protože n! > n, intuice naznačuje, že posloupnost
Tato posloupnost je rostoucí, protože
Limita plyne z jednostranného srovnání, viz sekce Limita a srovnání:
Uvažujme posloupnost
![]() .
.
![]()
Někteří lidé dokonce takto definují Eulerovo číslo. Řeknou, že Eulerovo číslo
Posloupnosti
![]()
Posloupnosti se pak vytvoří tak, že se místo x dosadí přirozená čísla,
jinak řečeno, umístěním bodů do grafů na místa, kde jsou x-ové
souřadnice celá čísla. Všechny vlastnosti teď záleží na tom, jak se tyto
body, umístěné s rozestupem 1, shodnou s periodou sinu a kosinu, což je
Platí pro tyto body nějaká providelnost, například takto?
![]()
Pravidelně nebo ne, může se stát, že body padnou na vlny takovým způsobem, že vzniklá posloupnost je monotonní?
![]()
Mohlo by se třeba stát, že se body začnou "vyhýbat" vrcholům a údolím, takže se posloupnost nakonec stane malá?
![]()
Mohly by body padnout na vlny tak, že posloupnost nakonec konverguje?
![]()
Všechny tyto otázky mají zápornou odpověď. Body padnou na vlny způsobem, který se stále mění a nikdy neopakuje, a nezačnou se vyhýbat žádné části sinové/kosinové vlny. Pokud si například vyberete určitou část základní vlny, pak ať už ignorujete jakkoliv velký začátek posloupnosti (sinové či kosinové, obě se chovají stejně), vždy se v konci najdou body, které padnou do této části, a když odříznete tuto část, zase se najdou body ve zbytku a tak dále. Následující obrázek ukazuje, jak to vypadá.
![]()
Co z toho plyne? Protože body mimo jiné znovu a znovu padnou na vrcholy a
údolí, posloupnosti nemohou být monotonní. Budou se také znovu a znovu
dostávat libovolně blízko k hodnotám 1 a
Pro podrobnější pohled na tuto problematiku klikněte sem.