Základní vlastnosti

Začneme tím, že se podíváme na několik základních vlastností limit. Pak se podíváme na věty o operacích, což vede přímo na algebru limit, náš hlavní nástroj k výpočtu limit. Pak se podíváme na vztahy mezi konvergencí a monotonií a omezeností; také se podíváme na limity a podposloupnosti. Nakonec stručně uvedeme pojem Cauchyovské posloupnosti.

Pár jednoduchých tvrzení

Následující tvrzení by vám měla být jasná, pokud chápete, co je to limita.

Fakt.
Posloupnost {a_n} konverguje k L právě tehdy, když {a_n − L} konverguje k 0.

Fakt.
Jestliže jde posloupnost {a_n} k L, pak {|a_n|} jde k |L|.

Fakt.
Posloupnost {a_n} jde k 0 právě tehdy, když {|a_n|} jde k 0.

Fakt.
Nechť posloupnosti {a_n} a {b_n} konvergují. a. Limita {a_n} je rovna limitě {b_n} právě tehdy, když {a_n − b_n} jde k 0.

Poznamenejme, že poslední tvrzení neplatí, jestliže vypustíme předpoklad o konvergenci.

Fakt.
Jestliže má posloupnost {a_n} nenulovou limitu, pak existuje N a konstanta m > 0 taková, že | a_n | > m pro k > N.

Při výpočtu limity jsou výchozím bodem elementární limity, které bychom si měli pamatovat; jsou to základní stavební prvky. Složitější výrazy jsou pak vytvořeny kombinováním těchto elementárních výrazů, proto potřebujeme ještě vědět, jak je spojovat v limitě.

Věta (limita a algebraické operace).
Předpokládejme, že posloupnost {a_n} má limitu A a posloupnost {b_n} má limitu B. Pak platí následující:
(i) Pro libovolné reálné číslo c, posloupnost {ca_n} má limitu cA, pokud to má smysl.
(ii) Posloupnost {a_n + b_n} má limitu A + B, pokud to má smysl.
(iii) Posloupnost {a_n − b_n} má limitu A − B, pokud to má smysl.
(iv) Posloupnost {a_n⋅b_n} má limitu A⋅B, pokud to má smysl.
(v) Posloupnost {a_n /b_n} má limitu A/B, pokud to má smysl.
(vi) Posloupnost {a_n ^b_n} má limitu A^B, pokud to má smysl.

Co jsou ty poznámky o smyslu? Pokud jsou A a B reálná čísla, neboli pokud jsou ty dvě posloupnosti konvergentní, pak mají operace (i) až (iv) vždy smysl. Na druhou stranu, podíl A/B má smysl jen pokud je B nenulové. A to je přesně to, co se tím myslí; můžeme tuto větu použít, pokud to, co nám na konci vyjde, má smysl. To, co jsme tu dostali, je vlastně rozšířením obvyklé algebry. Když jsme předtím napsali "3 + 2 = 5", měli jsme tím na mysli, že tři jabka přidaná k dvěma jabkům dají pět jablek. Teď to ovšem také může znamenat, že "když se posloupnost konvergující k 3 přičte k posloupnosti konvergující k 2, dostane se posloupnost konvergující k 5." Vzniká tak "algebra limit" a na rozdíl od algebry obvyklé, tato pracuje i s nekonečny.

Teď bychom mohli uvést větu se spoustami tvrzení, ale je mnohem lepší začít z opačného konce. Všimněte si, že v té větě výše jsme nikde nepředpokládali, že A,B jsou konečná, a některé operace lze definovat i pro případ, když se v nich vyskytuje nekonečno. Pokud ty operace použijeme v oné větě nahoře a považujeme je za "mající smysl", pak výsledky, které dostaneme, jsou správné. Jaké operace můžeme zavést?

Co na příklad dostaneme, jestliže sečteme či vynásobíme dvě hrozně velká čísla? Další ohromně velké číslo. Právě jsme vymysleli, že ∞ + ∞ = ∞ and ∞⋅∞ = ∞.
Lze se také zeptat, co se stane, když se nekonečna smíchají s normálními čísly. Například pokud odečteme 13 od opravdu ohromně velkého čísla, zůstane nám pořád ohromné číslo (milionář, který příjde o korunu, je pořád v zásadě milionář). A opravdu, pro libovolné reálné číslo L máme ∞ − L = ∞.

Co dostaneme, když odečteme ohromně velké číslo od jiného ohromně velkého čísla? To záleží. Mohou být stejně velké a dostaneme nulu. Nebo jedno může být větší, výsledek pak záleží na tom, které z nich a o kolik. To ukazuje, že rozdíl ∞ − ∞ může mít mnoho rozdílných výsledků, záleží na situaci. A opravdu, tato operace není definována, protože to nejde rozumně udělat. Takovým výrazům se říka "neurčité".

Úplný výpis všech operací, spolu s poznámkami a dalšími detaily, najdete tady. Mimo jiné tam najdete důležitou poznámku ohledně určitých omezení této algebry. Jinými slovy, rozhodně si tam klikněte. Pro stručný výpis algebry limit klikněte sem.

Poznamenejme, že "mít smysl" pro limity je trochu jiné než mít smysl pro čísla. Důvodem je, že čísla A,B teď nereprezentují reálná čísla, tj. pevné hodnoty, ale výsledky limit, jinými slovy, reprezentují procesy, "skoro čísla". To způsobuje, že některé operace, i když se dají dělat s reálnými čísly, nefungují s limitami. Nejlepším příkladem je mocnina 0⁰. Víme, že jako číslo to má smysl a dává to 1. Pokud ale tyto nuly reprezentují výsledky limit posloupností, pak jsme v situaci, kdy hledáme limitu obecné mocniny a_n ^b_n. Když je n blízko k nekonečnu, pak jak a_n tak b_n jsou blízko nuly, ale malé číslo umocněné na malé číslo nemusí být blízko 1, může to být něco velice malého nebo naopak hodně velkého, podle toho která "skoro nula" je blíž nule. Výsledek limity (tj. výrazu 0⁰ v limitní algebře) proto závisí na tom, jak rychle jdou a_n a b_n k 0, limita dokonce ani nemusí existovat. V algebře limit je 0⁰ neurčitým výrazem.

Neurčité výrazy jsou stejně důležité jako algebra limit. Když počítáte limity, je důležité vědět nejen co funguje, ale i co nefunguje. Pro úplný výpis neurčitých výrazů, spolu s poznámkami a více detaily, klikněte sem. Pro stručný výpis klikněte sem.

Jako poslední nabízíme zde nějaké poznámky ohledně operací s posloupnostmi, které nemají limitu. To už není tak zajímavé a uvádíme to zde spíš pro úplnost, popřípadě k uspokojení zvědavějšího čtenáře.

V praxi se řídíme velice jednoduchým pravidlem.

Pokud chceme najít limitu posloupnosti dané nějakým výrazem, tak do něj "dosadíme" nekonečno, a pokud mají příslušné operace smysl, tak je to, co vyjde, správnou odpovědí na tu limitu.

Je to ale nicméně dost neformální a někteří profáci jsou na to alergičtí. Nejlepší je udělat všechny "výpočty s nekonečnem" někde po straně. V našich výpočtech je budeme dávat - spolu s dalšími poznámkami - mezi dvojité lomené závorky ⟪ a ⟫, abychom zdůraznili, že nejsou součástí "oficiálního" řešení. Teď to ukážeme na velice jednoduchém příkladě, který uděláme podrobně, se všemi kroky; obvykle bychom jej řešili mnohem rychleji.

Jen zřídka dostaneme výsledek tak snadno, mimo jiné proto, že ty "malé kousky" jsou často drobet komplikovanějsí a neznáme jejich limity hned, ale musíme je nejprve zjistit a teprve poté je zkusit dat dohromady. Pak je výše uvedená věta formulována trochu nešikovně; je mnohem pohodlnější, kdy ji vyjádříme v této formě:

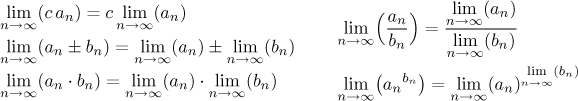
Důležitá poznámka: každá z těchto rovností platí jen tehdy, má-li výraz na pravé straně smysl. Jsou tedy "podmínečné": Dokud nevíme, že konečný výsledek určitého výpočtu má smysl, tak všechny rovnosti v něm nemusí být pravdivé. Jinak řečeno, nemá smysl rozdělit výraz na části, pokud výsledek nedává smysl. Například konstantní funkce 1 má v nekonečnu limitu 1. Když ji ale napíšeme jako 1 = (1 + n) − n a spočítáte limitu každé části zvlášť, dostanete něco, co nemá smysl: ∞ − ∞.

Teď ukážeme jednoduchý příklad.

Příklad: Najděte

Vidíme, že n se vždy vyskytuje v nějakém výrazu, jehož limitu v nekonečnu již známe (viz základní limity). Jmenovitě, konstanty 13 a 5 konvergují k sobě samým. Dále máme:
(i) Víme, že 1 dělená odmocninou z n, což je vlastně 1/n^1/2, konverguje k nule (n s kladnou mocninou je ve jmenovateli). Další způsob, jak to vidět: odmocnina z n jde do nekonečna a 1/∞ = 0.
(ii) Podle Věty o sevření (viz Limita a srovnání v části Teorie - Limita) víme, že (−1)ⁿ/n→0.
(iii) Víme, že n→∞.
(iv) Abychom viděli, jak vypadá druhý člen ve jmenovateli, si jej nejprve přepíšeme tak, aby měl kladnou mocninu: 2⁻ⁿ = 1/2ⁿ. Víme, že 2ⁿ je geometrická posloupnost jejíž základ 2 je větší než 1, takže jde do nekonečna. Následně 1/2ⁿ jde k 1/∞ = 0.
     Je také možné psát 2⁻ⁿ = 1/2ⁿ = (1/2)ⁿ. Teď je to geometrická posloupnost, jejíž základ 1/2 je (v absolutní hodnotě) menší než 1, takže tato posloupnost konverguje k 0.

Teď tyto částečné výsledky poskládáme dohromady podle věty o operacích a najdeme limitu dané posloupnosti. Podlé věty čitatel konverguje k 13 − 0 + 0 = 13, zatímco jmenovatel konverguje k ∞ + 5⋅0 = ∞. Celá posloupnost pak konverguje k 13/∞ = 0.

Teď si ukážeme, jak to napsat jednodušeji pomocí limitního symbolu. Vypíšeme všechny kroky, ať je vidět celá dekompozice krok za krokem, normálně bychom to napsali mnohem kratšeji.

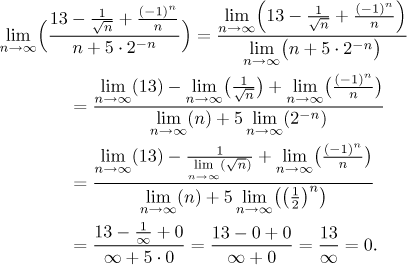
Toto řešení bylo správné, ale poněkud dlouhé. Aplikováním algebry limit a s pár výpočty po straně (mezi dvojitými lomenými závorkami) to zvládneme mnohem rychleji:

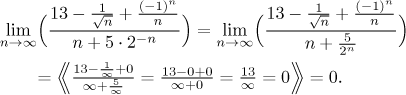
A to je můj oblíbený způsob řešení - korektní a krátký.

Pro další rady a lepší náhled na aplikaci této věty viz Přehled metod - Limita.

Věta.
Nechť {a_n} je posloupnost s limitou A, předpokládejme, že a_n ≠ A pro všechna n. Nechť f je funkce, která má limitu B pro x→A. Pak posloupnost {f (a_n)} má limitu B.

Zde A a B mohou být nekonečné, pokud výrazy, které z toho vyjdou, mají smysl. Nejtypičtější případ je, když A je číslo a f je spojitá v A, což prakticky znamená, že f je dána vzorcem, kterému nevadí, když do něj dosadíme A. V takovém případě můžeme vyjádřit větu takto:

Aplikace je snadná. Pokud hledáme limitu posloupnosti, která je ve tvaru "výraz uvnitř pěkné funkce", pak můžeme ignorovat tu funkci, najít limitu onoho výrazu uvnitř, pak tuto limitu dosadit do funkce. Jednoduchý příklad je zde.

Všimněte si, jak toto pěkně sedne k předchozímu příkladu s algebrou limit. Tam jsme na chvíli ignorovali operace a jen se soustředili na jednoduché členy, základní cihly, ze kterých byla posloupnost poskládána. Našli jsme jejich limity, pak jsme je poskládali dohromady a dostali konečný výsledek. Tato věta nám říká, že můžeme zpočátku ignorovat i funkce, najít limity jednoduchých výrazů, pak dát dohromady tyto částečné odpovědi nejen pomocí algerby limit, ale také substitucí do funkcí; pokud má výsledek smysl, tak je správně. Pokud se podíváte například na tento příklad, mělo by to být jasnější.

Ono praktické pravidlo - dosaď a uvidíš - lze tedy aplikovat i na výrazy se skládáním, je to obecné pravidlo pro limity, kterým vždy začínáme. Samozřejmě mnoho, snad i většina limit takto najít nepůjdou. Pak je třeba použít triků, které změní danou posloupnost v jinou, která už půjde vyřešit naší základní metodou - poskládáním částečných výsledků dohromady pomocí algebry limit.

Ještě jedno velice důležité pravidlo: Pokud si nejste naprosto jistí, že víte, co děláte, pak vždy dopočítejte všechny části. Například pokud rozdělíte limitu součinu na součin menších limit a jedna z nich vyjde nula, nemůžete přestat s výpočtem a prohlásit, že všechno je nula. Je sice pravda, že nula krát číslo je nula, ale to funguje jen v normální algebře. V algebře limit můžeme také mít "nula krát nekonečno", což je neurčitý součin, který může vyjít libovolně. Jako příklad zkusíme jiný rozklad 1:

lim(1) = lim((1/n)⋅n) = lim(1/n)⋅lim(n) = 0⋅∞.

Evidentně by bylo chybou skončit, už když jsme viděli, že první limita vyšla nula, po dopočítání druhé části totiž vidíme, že máme neurčitý součin, a z toho víme, že nebyl dobrý nápad rozdělit původní limitu na dvě. Pro další detaily viz tato poznámka.

Viděli jsme, že konvergentní posloupnost se může blížit k limitě podivným způsobem, takže se rozhodně nedá od konvergentních posloupností čekat obecně nějaká monotonie. S omezeností je to nadějnější:

Věta.
Každá konvergentní posloupnost je omezená.

Můžeme dostat nějakou informaci ohledně konvergenci z našich dvou základních vlastností? Ekvivalentní verze poslední věty říká, že neomezená posloupnost musí být divergentní, to je nějaká informace. Můžeme dostat i něco pozitivního? Kdepak. Příklad alternující posloupnosti ukazuje, že omezená posloupnost nemusí konvergovat, limita dokonce neexistuje vůbec (ani nevlastní). Nicméně pokud jsme ochotni ztratit některé členy dané posloupnosti, pak už něco z omezenosti dostaneme (srovnejte Bolzano-Weierstrassovu větu v sekci Funkce - Teorie - Reálná čísla - Topologické pojmy):

Věta (Bolzano-Weierstrassova věta).
Každá omezená posloupnost má konvergentní podposloupnost.

Další užitečná vlastnost je monotonie. Když si zkusíte představit různé rostoucí posloupnosti, měli byste začít mít (správný) pocit, že takové posloupnosti buď rostou směrem k nějaké horní mezi, která se pak stane jejich limitou a ony konvergují, nebo rostou nade všechny meze a proto jdou do nekonečna; každopádně mají limitu. To je opravdu správně, navíc omezenost nabízí pěkný způsob, jak se vyhnout tomu nekonečnu.

Věta.
Každá monotonní posloupnost má limitu.
Každá omezená monotonní posloupnost má limitu.

Detailněji, každá neklesající posloupnost (a tedy každá rostoucí posloupnost) buď konverguje nebo jde do nekonečna, a každá nerostoucí posloupnost (a tedy každá klesající posloupnost) buď konverguje nebo jde do mínus nekonečna.

Začneme s teoretickým výsledkem.

Věta.
Jestliže daná posloupnost konverguje, pak všechny její podposloupnosti konvergují k téže limitě.

To nám při zkoumání zrovna dvakrát nepomůže, ale následující slabší tvrzení v jakoby opačném směru je často užitečné.

Fakt.
Jestliže daná posloupnost má dvě podposloupnosti, které konvergují k rozdílným limitám, pak daná posloupnost diverguje.

Například z alternující posloupnosti {1, −1, 1, −1, 1, −1, 1,...} lze vybrat všechny liché členy a zformovat podposloupnost {1, 1, 1, 1, 1,...} konvergující k 1, ale také lze vybrat všechny sudé členy a tak dostat podposloupnost {−1, −1, −1, −1, −1,...} konvergující k −1. Podle citovaného faktu alternující posloupnost diverguje.

Někdy se dá u posloupnosti zpozorovat užitečná vlastnost, že jak pokračuje, tak se mění méně a méně. Při formální definici zase použijeme přístupu přes hry. Někdo nám zadá toleranci a my chceme být schopni vyhodit nějaký začátek dané posloupnosti tak, aby se její zbývající členy neměnily o víc než ona tolerance.

Definice.
Uvažujme posloupnost {a_n}. Řekneme, že je to Cauchyovská posloupnost, nebo že tato posloupnost je Cauchyovská, jestliže pro každé ε > 0 existuje přirozené číslo N takové, že pro všechna m,n ≥ N máme |a_n − a_m| < ε.

Pokud posloupnost konverguje, tak se usadí u nějaké hodnoty a už se moc nemění. To se zdá jasné a je to opravdu snadné dokázat. Méně snadné je dokázat (např. pomocí Bolzano-Weierstrassovy věty výše), že pokud se posloupnost usadí, pak by měla konvergovat (což zase vypadá jako selský rozum). Dostaneme tedy následující větu.

Věta.
Posloupnost reálných čísel konverguje tehdy a jen tehdy, jestliže je Cauchyovská.

Všimněte si, že tato věta dává jen konvergenci, nikoliv konkrétní hodnotu limity, což naznačuje, že je to spíš výsledek teoretický než praktický. A je to tak, v teorii je nenahraditelný a velice užitečný v mnoha situacích.

Zmínili jsme se, že jedna implikace je méně triviální. Zatímco konvergentní posloupnosti jsou Cauchyovské také pro posloupnosti s členy z velice obecných protorů, fakt, že Cauchyovské posloupnosti konvergují, není automatický. Pokud například pracujeme v oboru racionálních čísel, tak už to neplatí (viz úplnost v části Extra - Množiny a zobrazení - Důležité číselné množiny). Tvrzení, že Cauchyovské posloupnosti reálných čísel konvergují, se někdy nazývá Bolzano-Cauchyova věta.

Limita a srovnání
Zpět na Teorie - Limita