Domain of a real function: Survey of methods

Whenever we are exploring a given function, we start by determining its domain, since all calculations will be done with respect to this domain.

To find the domain, we try to answer the following question: What numbers could cause troubles in the expression that defines the function? Since a typical function is actually just a bunch of elementary functions put together by composition and/or algebraic operations, we scan all present functions and operations, some of them will cause restrictions for the variable.

In order to do this effectivaly we have to be familiar with domains of elementary functions. We also have to remember that all general powers (that is, powers that feature x both in the base and the exponent) and roots have to be first transformed using the z = e^ln(z) trick, only then can we do the analysis.

List of the typical problems:

• in a fraction, the denominator must not be zero;
• the argument of a logarithm must be positive;
• the argument of an even root must be non-negative (that is, positive or zero);
• the argument of a power with a general (real) exponent must be positive;
• the argument of tangent cannot be  + kπ, the argument of cotangent cannot be kπ;
• the argument of arcsine and arccosine must be from the interval [−1,1];
• the argument of hyperbolic cotangent cannot be zero;
• the argument of argcosh must be from the interval [−1,∞);
• the argument of argtanh must be from the interval (−1,1);
• the argument of argcoth must be from the interval (−∞,−1) ∪ (1,∞).

Other elementary functions (that do not appear on this list) have all real numbers as their domain, therefore they do not force any restriction on the domain.

So we scan the given expression for these sources of trouble, each will give us a condition to solve. The solutions will then be intersected to form the domain. Why intersection? In order for the given function to exist, all its parts must exist simultaneously.

In fact, the only non-trivial part of finding domains is solving the inequalitites one gets. If you need a refresher on this high-school topic, try Solving equations and inequalities in Extra.

Before we move on to an example, I feel one explanation is in place. That example looks scary, but that's intentional. It is definitely not a "typical" example on domains, those you find in the section Solved Problems and in Exercises. Here we are in Methods Survey, we will instead look at a function with lots of problems and survey them. There is another angle to this example. Although it looks terrible, when you look closer, you will find that it is actually not more difficult than "typical" problems, just longer, since there is more things to work out. This example also shows the need to get organized. If you can do it and if you studied your domains well, then this example may actually encourage you when you find out that you can handle even such a beast. And if you can do this, you can do anything that comes your way. Enough pep talk, let's go.

Example. Find the domain of

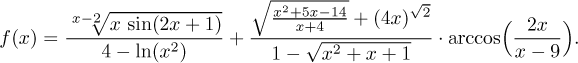
Solution: First we have to rewrite the function so that it does not feature the general power.

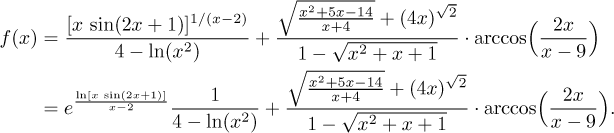
Now we will scan it for sources of trouble. There are quite a lot of polynomials, but these can take any argument, so they do not worry us. We also know that the exponential and the sine can take any argument, so no problem there either. What are the problems? Let's take it from the left.

1. In the exponential we see a fraction, its denominator cannot be zero. Thus we get the condition (x − 2) ≠ 0.
2. In the same exponential, we see a logarithm. Its argument must be positive, so we get the condition x⋅sin(2x + 1) > 0.
3. Next comes the fraction, we know that its denominator must not be zero; thus we get the condition (4 − ln(x²)) ≠ 0.
4. In this very denominator, we have a logarithm, so the condition is x² > 0.

5. Next comes another fraction, which means another condition on the denominator:

   

6. In this same denominator we have a square root, the condition is (x² + x + 1) ≥ 0.

7. In the same fraction we have a square root in the numerator; this requires that

   

8. The fraction under this root requires that (x + 4) ≠ 0.
9. Still in the numerator, next to the fraction is (4x) raised to the power "root of 2". Since the power - the root of 2 - is a positive real number, not some special case (like a positive integer), we have to ask that (4x) ≥ 0.

10. Finally we are getting to the arccosine. Here the condition is

    

11. And really finally, in this fraction we must ask that the denominator be non-zero, that is, (x − 9) ≠ 0.

This concludes the list of problems. Now we have to solve these 11 conditions.

Condition 1. This clearly reads x ≠ 2.

Condition 2. We have a product of two terms, and we know that for a product to be positive, there are two possibilities: Either both terms are positive, or both of them are negative. We can come to the same conclusion if we think of another way to solve this inequality. We can think of dividing both sides of x⋅sin(2x + 1) > 0 by the x, which would simplify the inequality quite a bit. However, when dividing (or multiplying) an inequality by a number, we have to check whether it is positive or negative, and in the latter case switch the inequality to its opposite. Here we don't know, so we need to check both cases and put the answers together. Either way, the solution is

For details see this page.

Condition 3. We rewrite this condition to ln(x²) = 4. We can apply the exponential to both sides of this equation to get e^ln(x2) = e⁴, that is, x² = e⁴. This has two solutions, x = e² and x = −e². Thus the solution to the third condition is x ≠ ±e².

Note that algebraically we could write ln(x²) = 2ln(x), but from the point of view of functions these are two very different things. While the first expression (which we were given) exists for all x ≠ 0, the second one exists only for x > 0. As a consequence, while ln(x²) = 4 has two solutions as we saw above, the equation 2ln(x) = 4 has only one solution, x = e²! This shows that one has to always solve the given expression, and if we want to change it somehow algebraically, we can only do changes that do not affect the domain, otherwise we may lose some solutions (or get some extra wrong ones).

Condition 4. This condition has an easy solution x ≠ 0.

Condition 5. We rewrite this condition to the form

Thus we get two conditions, x ≠ 0 and x ≠ −1.

Condition 6. We check that the polynomial x² + x + 1 has no roots, therefore it is either always negative or always positive. Since its graph is an upward oriented parabola (the sign in front of x² is "+"), the latter is true. The expression x² + x + 1 is positive for all real numbers and therefore no restriction on x follows from the sixth condition.

Condition 7. This type of inequality is best solved by factoring and then determining signs of individual factors. It is also possible to try to multiply the inequality by the denominator, but this would require that we try both possibilities of sign for this denominator, that is, we would have to solve the inequality twice. Either way, the answer is

x∈[−7,−4) ∪ [2,∞).

For details see this page.

Condition 8. This clearly reads x ≠ −4.

Condition 9. Here the condition clearly reads x > 0.

Condition 10. The condition actually involves two inequalities that have to be satisfied simultaneously. There are two reasonable strategies. One is to get rid of the fraction by multiplying. This can be done simultaneously for both inequalities, the easier inequalities that thus arise are then solved individually. Disadvantage of this approach is that one has to do it twice, for positive and negative denominators.

An alternative would be to solve each inequality separately, best by changing it into an inequality with "0" on one side and some product/ratio of linear factors on the other side, since then one can use the chart method of determining signs. Either way, the answer should be

x∈[−9,3].

For details see this page.

Condition 11. This clearly reads x ≠ 9.

It remains to put all these conditions together. Since in order to exist, the function must have all parts without trouble, we take the intersection of all eleven conditions. This is done best graphically.

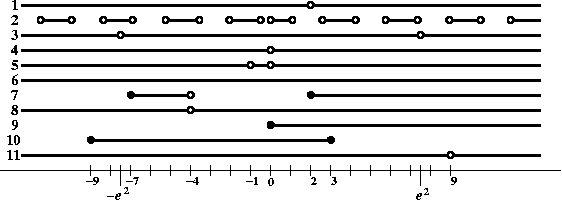
Thus the conclusion is that

For more examples we refer to Solved Problems.

Boundedness
Back to Methods Survey - Basic properties of real functions