Problem: Determine the symmetry of the following function:

Solution: First we determine the domain of this function. There are two sources of trouble. One is the square root, but the expression under it satisfies x² + 1 ≥ 1 > 0, so no problem there.

Next we check on the logarithm. Its argument must be positive, but here it is not so simple to check where it works. "Standard" approach would be to find the zero points of this expression and determine its signs (see also this solved problem). In this case there are no zero points, so this expression is either always positive or always negative. Trying x = 0 we see that the former is true and there is no restriction on the domain. Another possible way to argue is this: Since x² + 1 > x², it follows that the square root is larger than |x|, therefore after adding x to it we surely get something positive. We include two more ways to handle this in the Note at the end of this problem

Anyway, we see that this function has the whole real line as its domain, and since it is a symmetric set, there is a chance that the given function is symmetric. We try the usual approach, substituting (−x) for x.

Now we are in a bit of trouble. It would seem that we cannot pull the minus out nor make it go away, so perhaps this function is not symmetric at all. However, such "feelings" might be wrong and we need to know for sure. Then the best thing to do is to check on both kinds of symmetry using equalities. First we try whether the function is even, we will try to get rid of logarithms by raising both sides to an exponential and cancelling "e^ln":

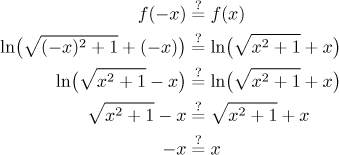
We have an equality that is not true for all x from the domain (that is, for all real x), so the original equality is not valid and the function is not even. Now we try for being odd. To use the "e^ln" cancelling, we will have to make log to be the outermost function on the right.

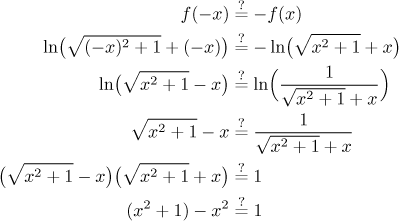
Now we have an equality that is true for all real x, so surprisingly enough, we just proved that this function is odd.

In fact, now that we know that this calculation involves the complementary "root minus x" term, we can also show it directly:

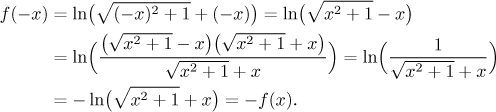
So indeed, this function is odd.

Note: Here we show two more ways to prove that the expression "root plus x" is always positive.

One way to argue is this: There are two cases. If x is positive, then the whole expression is clearly positive. If x = 0, then substituting into the expression gets us 1, which is surely positive. What if x is negative? Then the term "root minus x" is surely positive, so we can multiply the required inequality with it without changing the direction of inequality:

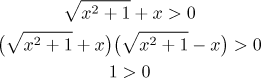
We obtained a true inequality and the operations were equivalent, so the original inequality was valid, that is, the investigated term is positive also for x < 0.

The second alternative way is this: We might be tempted to move x to the other side of the inequality

and then get rid of the annoying root by squaring both sides of the inequality. Unfortunately, this operation does not work in general. It only works if we know for sure that the signs of the terms on both sides are positive. One can also square both sides if the two sides are negative, but then it is necessary to switch the direction of the inequality. In short, squaring inequalities is a risky business and if you can avoid it, do it.

However, if you are good at math, you may try your hand at it and get a shorter solution. What can we say about the signs of the two sides of our inequality? The left-hand side is positive, so we can only square both sides if the other one is also positive, that is, if -x > 0. Thus squaring can be done if x < 0, but fortunately for us, this is exactly the non-trivial case, since as we saw above, for x positive or zero the required inequality is clearly true. So we assume that x < 0 and square:

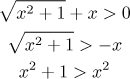
Again, we obtained an inequality that is always true, which is another confirmation that the logarithm makes sense for all x.

Next problem
Back to Solved Problems - Real functions