Integrální kritérium, aproximace

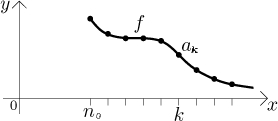
U typické řady jsou členy a_k dány nějakým vzorcem. Tento vzorec má obvykle smysl nejen pro celá čísla k z oboru indexace, ale také pro reálná čísla mezi nimi; vzorec tedy definuje nějakou funkci f na intervalu ⟨n₀,∞) a jednotlivé členy řady jsou jen určité speciální hodnoty této funkce, a_k = f (k).

Existuje nějaký vztah mezi chováním takové řady a chováním této funkce f? Za určitých okolností to možné je.

Věta (integrální kritérium).
Předpokládejme, že f je kladná a nerostoucí funkce na nějakém intervalu ⟨n₀,∞) pro určité celé číslo n₀. Pro všechna celá čísla k ≥ n₀ definujeme a_k = f (k).
Pak řada  a_k  konverguje tehdy a jen tehdy, když nevlastní integrál    konverguje.
Navíc pak máme

Proč by mělo něco takového platit? Klíčové pozorování je, že když vidíme člen a_k této řady, můžeme to interpretovat jako plochu obdélníka s výškou a_k a základnou 1. To můžeme samozřejmě udělat s každým číslem, ale ten opravdický trik je najít vhodný objekt, na který ten obdélník aplikujeme. Rozhodneme se použít ten obrázek výše a umístit tento konkrétní obdélník tak, aby jeho horní levý roh ležel na bodě označujícím a_k. Jeho základna pak leží na ose x. Uděláme to se všemi členy řady.

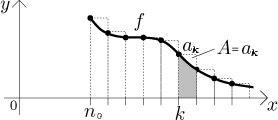
Teď se znovu podívejme na obdélník přiřazený k a_k. Protože je f nerostoucí a prochází levým horním rohem tohoto obdélníka, vyplývá z toho, že integrál f mezi k a k + 1, tj. obsah pod f mezi těmito dvěma čísly, nemůže převýšit obsah našeho obdélníka, což je a_k. Tímto způsobem najdeme vztah mezi jistým určitým integrálem f a členem a_k. To můžeme udělat pro všechny členy řady a pak sečíst vzniklé nerovnosti, dostaneme

Vidíme tedy, že pokud je integrál divergentní, tedy nekonečný, pak řada také musí dávat nekonečno. Naopak pokud řada konverguje, pak musí integrál také konvergovat (zde se silně spoléhá na to, že f > 0, takže nám integrál nemůže utéct do záporné části). Tím jsme dostali jeden směr, jeden odhad pro řadu. Mimochodem, korektní matematický důkaz vypadá prakticky stejně, jen je to třeba trochu vyčistit, hlavně si musíme ohlídat konvergenci (přejít k částečným součtům a tak). Ten hlavní nápad jsme ale vysvětlili správně.

Zbývá odůvodnit druhý směr neboli horní odhad pro řadu. Tentokráte umístíme obdélníky tak, aby body řady byly v jejich pravých horních rozích. Tímto způsobem se obdélník přiřazený k a_n0 ocitne mimo f, takže jej vyřadíme.

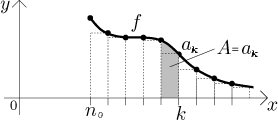
Obsah a_k je teď omezen shora integrálem f od k − 1 do k.

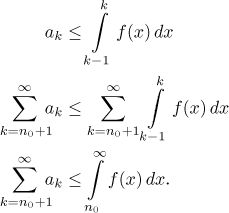
Teď jen přidáme a_n0 na obě strany této nerovnosti a dostaneme žádaný odhad. Vidíme také, že když řada dává nekonečno, pak také integrál musí být nekonečný. Na druhou stranu, pokud integrál konverguje, pak když vezmeme v úvahu, že nám řada nemůže utéct do záporných čísel, dostaneme závěr, že musí také konvergovat.

Poznamenejme, že podle poslední nerovnosti ve výpočtu také můžeme dostat tento horní odhad pro naši sumu:

Mnozí autoři (možná většina z nich) dokonce dávají do svých verzí integrálního kritéria právě tento horní odhad, protože vyplyne přímo z důkazu. Nikdy ale nedává lepší výsledky než naše verze a ve většině případů dokonce funguje hůř, takže nic neztratíme, když to tu budeme ignorovat.

Poznámka: Ve větě jsme použili n₀ jako počátek naší indexace. Když nás ale nezajímá odhad, jen konvergence či divergence, tak víme, že je tento začátek irelevantní. Integrální test pak lze zjednodušit následovně: Řada  ∑ a_k  konverguje tehdy a jen tehdy, když integrál odpovídající funkce f od nějakého vhodného K do nekonečna také konverguje (za předpokladu, že f je kladná a nerostoucí, jinak nelze tento test použít).

Příklad: Teď dokážeme, že řada konverguje.

Vzorec v řadě také definuje funkci f (x) = 1/x², která je kladná a klesající například na ⟨1,∞). Můžeme proto použít integrální kritérium. Protože víme, že tato funkce má na daném intervalu konvergentní integrál, podle integrálního kritéria vyplývá, že daná řada konverguje.

Poznámka: Konvergenci této řady bychom si správně měli pamatovat, obvykle se odkazujeme na p-test, viz Teorie - Úvod - Důležité příklady. Samotný p-test se dokazuje přímou aplikací integrálního kritéria. Stačí nahradit číslo 2 písmenem p v úvaze výše a pak se podívat na konvergenci integrálu (v nekonečnu) funkce f (x) = 1/x^p, viz také Vlastnosti neurčitých integrálů v části Integrály - Teorie - Nevlastní integrál.

Pěkný příklad na použití integrálního kritéria lze najít v Přehledu metod a další v části Řešené příklady - Testování konvergence, jmenovitě tento příklad, viz také tento příklad.

Ony dvě nerovnosti v integrálním kritériu nám také umožňují aproximovat součet v případě, že nejsme schopni najít přesnou hodnotu (což je obvyklá situace). Všimněte si, že rozdíl mezi horním a dolním odhadem je přesně a_n0. Víme, že členy konvergentní řady jdou k nule, což nám říká, že dostáváme přesnější odpověď, pokud tento odhad aplikujeme pouze na konec dané řady. Podívejme se na následující příklad.

Dokázali jsme, že řada konverguje. Teď zkusíme odhadnout její součet pro případ, kdy indexace začíná v 1. Vlastně díky pokročilé matematice víme, kolik to ve skutečnosti je, viz příslušný příklad v sekci Důležité příklady v části Teorie - Úvod do řad, ale tento vysledek byl získán velice specifickým trikem. Zde máme relativně jednoduchou metodu s mnohem větším potenciálem použití.

Podle integrálního kritéria máme

Dostali jsme odhad, ale není příliš přesný. Vzhledem k tomu, že výsledek je zhruba 1, je chyba velikosti 1 příliš velká. Řekněme, že chceme chybu nejvýše 0.005. Protože je chyba dána členem 1/n₀², tak vidíme, že k potlačení chyby na dostatečně malou hodnotu potřebujeme začít sčítat od 15 (či dále). Co se stane se začátkem řady, který jsme vynechali? Ten začátek je vlastně konečná suma, tudíž ji můžeme přesně spočítat a přičíst ke všem částem oné dvojité nerovnosti.

Můžeme si tipnout, že součet je asi 1.645, a nebudeme příliš daleko. Metoda, kterou jsme použili, se dá obecně vyjádřit tímto vzorcem:

Rozdíl mezi horním a dolním odhadem je a_K, což jde pro konvergentní řadu k 0, takže dostaneme odhady s libovolnou přesností jen tím, že vezmeme dostatečně velké celé číslo K.

Srovnávací kritéria
Zpět na Teorie - Testování konvergence