Příklad: Určete, zda následující řada konverguje.

Řešení: Členy této řady jsou kladné, takže můžeme použít všechny ty báječné testy, a jako posloupnost jdou evidentně k nule, takže je tu šance na konvergenci. Všimněte si, že chování této řady závisí na parametru p, takže se dá čekat, že i odpověď bude na p záviset.

Jaká kritéria můžeme použít? Protože v členech této řady vystupují jen k a logaritmus, zkušenost naznačuje, že není dobrý nápad zkoušet odmocninové kritérium nebo podílové kritérium. A opravdu,

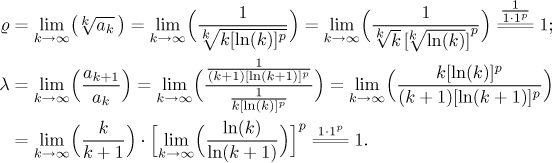
V obou případech dostáváme neurčitou odpověď 1. Mimochodem, v oněch limitách jsme použili následující výpočty k vyřešení neurčité mocniny a neurčitého podílu:

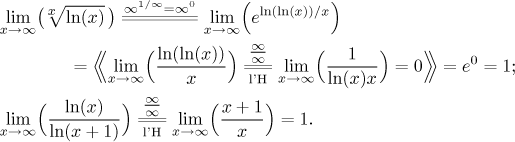
Často nám dobře poslouží srovnání. Zde se můžeme zkusit zbavit logaritmu. Protože jeho vynechání podstatně změní podstatu členů, nemůžeme použít limitní srovnávací kritérium (kde říkáme, že a_k je v zásadě jako b_k), ale můžeme doufat, že zabere obyčejné srovnání. Všimněte si ale, že když tu logaritmickou část vynecháme, tak nový výraz může být větší i menší - podle hodnoty p.

Za prvé, pokud je p záporné či nula, pak máme

Víme, že řada napravo diverguje, protože je to ta slavná harmonická řada nebo použijeme p-test. Daná řada je ještě větší, takže podle srovnání musí také divergovat. Teď už tedy víme, co se stane, když je p nejvýše nula. Což takhle když je p kladné? Pak máme

Srovnání teď jde špatným směrem a nemůžeme říct nic. Dá se získat nějaký odhad zdola? Vlastně ano, protože víme, že mocniny přebijí logaritmy. To znamená, že pro velká k můžeme logaritmickou část majorizovat pomocí mocniny s libovolným kladným exponentem c:

Protože nechceme při tomto srovnání ztratit příliš mnoho, zkusíme vzít c velmi malé (nerovnost pak platí jen pro velmi velká k, ale to stačí), ale ať už vezmeme jakkoliv malé c, vždycky ztrácíme příliš. Je to vidět z toho, že podle p-testu řada napravo konverguje pro libovolné 1 + c > 1, takže máme napravo konvergentní řadu a srovnání je na nic, nerovnost jde špatným směrem. Vidíme, že srovnání nepomůže pro kladné p.

Nakonec se tedy obracíme ke kritériu, které je méně populární, ale tady je jasnou volbou, jmenovitě k integrálnímu kritériu. Funkce f (x) = 1/(x[ln(x)]^p) je pro velká x kladná a klesající, můžeme tedy přejít k integrálu.

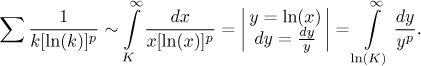
Teď nám p-test říká, že integrál konverguje, přesně když p > 1, a totéž je pak pravda i o řadě.

Závěr: Daná řada konverguje tehdy a jen tehdy, když p > 1.

Zkušený řešič řad by samozřejmě rovnou skočil po integrálním kritériu, ale pak bychom přišli o to napětí a krásný způsob, kterým nám srovnání dokázalo divergenci pro p záporné či nulové.

Je nějaká alternativa? Popravdě řečeno je, v sekci Další kritéria v části Teorie - Testování konvergence jsou k nalezení kondenzační testy, které tu mohou pomoci. O kladnosti a klesajícnosti členů už jsme se zmiňovali, takže technické předpoklady Cauchyho kritéria jsou splněny. Ten nám umožňuje přejít k řadě

Teď použijeme p-test a dostaneme stejnou odpověď, jmenovitě že tato řada a tudíž i daná řada konvergují, přesně když p > 1.

Můžeme také použít Jermakovovo kritérium.

Vidíme, že jestliže p < 1, pak r = ∞ a proto daná řada diverguje. Jestliže p > 1, pak pomocí l'Hôpitalov pravidla (nebo pravidla "mocniny přebijí logaritmy") dostaneme, že r = 0 a daná řada konverguje. Všimněte si, že tento test selhává pro p = 1.

Další příklad
Zpět na Řešené příklady - Testování konvergence