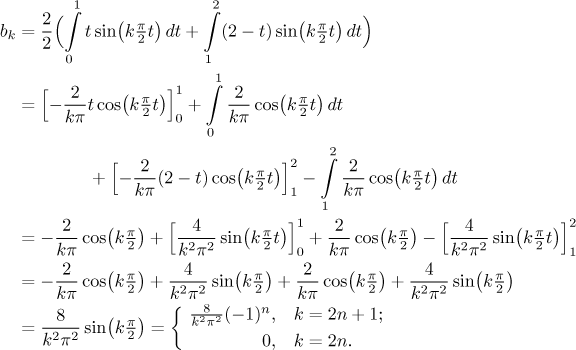
4: For the function of length L = 2, the sine and cosine expansions have double the length of period, that is T = 2L = 4, and the special frequency ω = π/2. Probably the easiest way to find the necessary coefficients is to use the standard formula, with L in place of T and the new special ω.

The sine series has a_k = 0. For the other coefficients you should get (using integration by parts)

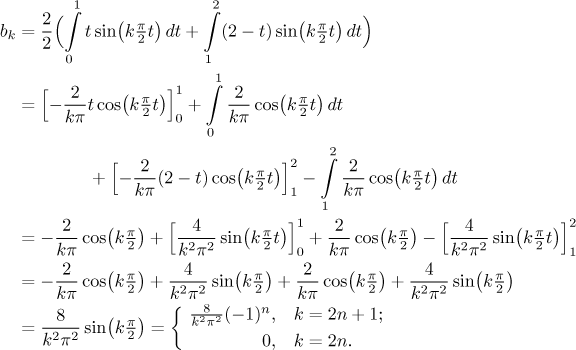
Use them to create the appropriate series. Then draw the odd periodic extension of f and apply Jordan's conditions to find the sum of this series.

The cosine series has b_k = 0. For the other coefficients you should get (using integration by parts)

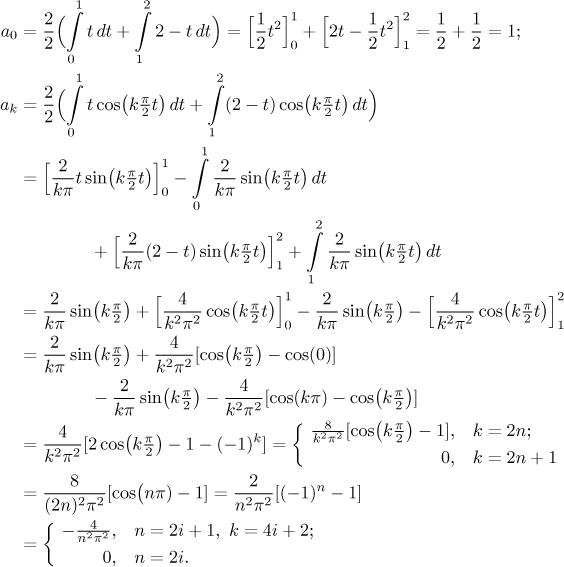
Use them to create the appropriate series. Then draw the even periodic extension of f and apply Jordan's conditions to find the sum of this series.

This is actually the same as the original Fourier series. This should be no surprise, since the usual periodic extension of f is already even. Thus there was no need to actually do the cosine expansion again, we could have just copied the Fourier expansion. However, it was not completely useless: It was a good exercise and a confirmation that things work as they should.

Answer