Fact.
Let
For all integers
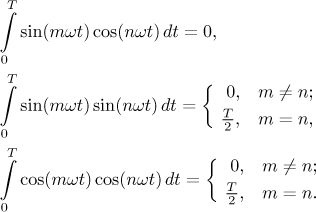
Here we will introduce trigonometric series and investigate possibility of expressing a function using such series. First we work on the whole real line and introduce the theory behind Fourier series. Then we apply this to functions on intervals and introduce the concept of sine and cosine Fourier series.
The underlying idea of Fourier series is to investigate what can be done
with sines and cosines. These naturally live on the interval
First, what are the values of k in the above system? Recall (see
Systems of functions) that we want
to obtain the largest result with the smallest possible set, so we
definitely want a linearly independent set. Now since the sines
in the above set are all odd functions and cosines are even functions, we
should not use negative integers for k, since then we would only
double functions that are already in the system, thus spoiling independence.
If
Note that there are in fact lots of trigonometric systems, they correspond to different choices of T. We do not mix them together, so when we talk about a trigonometric system, it is always assumed that it is a system that corresponds to some fixed positive T (and the corresponding frequency omega).
Having clarified this, it is now a standard fact that the sines and cosines in a trigonometric system form a linearly independent set. However, there is a deeper way in which these functions are distinct. In many areas of mathematics the following criterion is used to judge how far functions are from each other. Given two functions f and g on an interval I, we multiply them and integrate this product over I. The larger the resulting number is (in absolute value), the more do these two functions have in common. Obviously, the largest independence of these two functions occurs if this integral is zero, it corresponds to vectors being perpendicular. And that is exactly what happens for two distinct functions from our system.
Fact.
LetT > 0, denoteω = 2π/T.
For all integersm,n > 0 the following are true.
There is one more function in the trigonometric system, the constant function
The above property of perpendicularity makes the trigonometric system very special and in particular it comes handy when we address one of the the core question of this section: How do we express other functions using trigonometric functions? When expression functions using this system, the starting point is traditional linear combinations of functions from the trigonometric system, but the main object will be "infinite linear combinations" - that is, series. There are many ways in which the sines and cosines can be arranged and ordered, but one turned out to be the most practical; we will now set up the forms that we will use in the sequel.
Definition.
LetT > 0, denoteω = 2π/T.
By a trigonometric polynomial of degree N we mean the function
By a trigonometric series we mean the function series
where ak and bk are real numbers.
What functions can be expressed by series of this form? As usual, this is a very difficult question and we will apply the traditional approach. We will assume that a certain function f was already expressed as such a series and then we will try to find out what it means for this f and the series.
We start with something simple. Note that all functions in a trigonometric
system are
Fact.
LetT > 0, denoteω = 2π/T. Assume that for all real numbers t we have
Then f is necessarily
T-periodic.
Consequently, if we want to express functions f using trigonometric
series, then it is pointless to try other functions than periodic ones.
Thus in particular it is enough to do our investigations on the interval
Theorem (uniqueness).
LetT > 0, denoteω = 2π/T. Assume that f is aT-periodic function such that for all real numbers t we have
Moreover, assume that convergence of this series is uniform on
[0,T ]. Then the coefficients in this series are necessarily given by
Actually, note that also a0 is given by the second
formula, since for
We called this theorem the "uniqueness theorem", since it says that a periodic function can be expressed as a trigonometric series in only one way. However, note that we have uniqueness only for the case when the series converges uniformly. Otherwise it may happen that a function can be expressed as a trigonometric series and this series is not the one from the above theorem. This is quite different from the behavior of power series. The core cause for this difference lies in the fact that for power series convergence already implies uniform convergence (on almost whole region of convergence), which yields uniqueness in all cases. Here it can happen (and it does happen quite often) that we have convergence but not uniform convergence.
Note also that this uniqueness refers only to series whose basic
period is T. If the function f is also
Now we know that if we want to expand a function using a trigonometric series, the only way that has a good chance of succeeding is to use the coefficients as above. In order to do that we need to make sure that the integrals actually exist. (We did not have to worry in the above theorem, since uniform convergence of a series whose terms are continuous yields a continuous - hence integrable - function.)
Definition.
Let f be aT-periodic function for someT > 0, denoteω = 2π/T. Assume that f is Riemann integrable on[0,T ].
We define the Fourier series of f as the series
where the coefficients are given as
Note that this is a purely formal assignment. Given f, we calculate those integrals and create a series, but there is no guarantee that this series actually converges and if it does, that it converges to f. We denote this formal assignment as follows.

What good can be expected of this series? Convergence of Fourier series is very tricky and difficult, mathematicians have been working on it for over a hundred years. Obviously here in Math Tutor we are far from the level needed to understand all that, so we will just outline some useful results. For starters, note that even if f is continuous, then its Fourier series need not converge to it; as a matter of fact in a typical case it will not, often it even does not converge at all in many points. This does not sound too promising. From practical point of view some results are hopeful, though. They show that for convergence we need to look deeper into f, but then on the other hand we do not mind a little discontinuity here and there.
Theorem (Dirichlet).
Let f be aT-periodic function for someT > 0, denoteω = 2π/T. Assume that f is Riemann integrable on[0,T ]. Let
Assume that f is differentiable on a reduced neighborhood of some t0 and that this derivative has one-sided limits at t0. Then the Fourier series of f converges at t0 and
Recall that f (t0+) stands for the limit from the right at t0, f (t0-) denotes the limit from the left at t0,
This theorem has three important aspects. First, the convergence of the Fourier series can be deduced from differentiability, which is often used. Second, this convergence (and the value of this limit) depends only on behavior of f around the point t0. This means that for behavior of the Fourier series at t0 it makes no difference how f looks further away from this point. Results of this form are called principle of localization.
It also means that the value of f at t0 itself is irrelevant. Indeed, it does not appear at all in the above theorem, not even indirectly, and it actually should not be surprising. Since the coefficients of a Fourier series are given by integrals, it follows that we can change the given function at finitely many points without changing the resulting series.
The third important aspect is that the Fourier series recovers not the original function, but a sort of average of it. Given t0 as above, the Fourier series looks a bit to the left and a bit to the right and then it chooses exactly the middle value.
As we saw, Fourier series does not yield exactly the function value but the limit of it. Still, in practical use it would be nice to have an actual equality between f and its Fourier series. There is only one way to make this happen, we have to make the function value equal to the one-sided limits - and this means continuity.
Theorem.
Let f be aT-periodic function for someT > 0, denoteω = 2π/T. Assume that f is Riemann integrable on[0,T ]. Let
If f is differentiable at some t0, then
Now we will look at a global statement. We will not require continuity everywhere (since Fourier series are especially interesting for non-continuous functions), but in order to get something reasonable we cannot allow the function to have too many problems. One possibility to do this is as follows. We want the function to consist of "nice" pieces, that is, on every piece we expect the function to be continuous and perhaps to have some other favourable property. At endpoints of every piece we want one-sided limits to converge. For more precise definition, see for instance this note. The key property is that of bounded variation, the convergence of Fourier series is then guaranteed by the Jordan theorem. However, determining this property is not easy, so in applications we often prefer to check on stronger but more tractable properties.
Theorem (Jordan conditions implied by derivative).
Let f be aT-periodic function that is piecewise continuous with piecewise continuous derivative. Denoteω = 2π/T. Let
Then for every t we have
If f is actually continuous on the real line, then the Fourier series converges uniformly to f on the set of real numbers.
Recall that the idea behind the notion of a piecewise continuous and differentiable function is this: Its domain (in our case the real line) can be split into intervals (in our case infinitely many) whose lengths do not become arbitrarily small such that on interior of each interval the function is continuous, differentiable, this derivative is continuous, and the function and the derivative have proper one-sided limits at endpoints of these intervals. As an example, in the following picture we first show a typical function as in the assumptions of the above theorem and then how the sum of its Fourier series would look like.
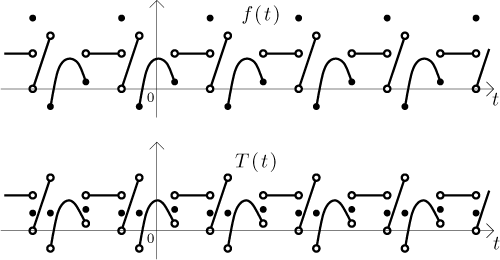
As you can see, the series returns the original function on the continuous segments, but at points of discontinuity it returns the average of the left and right limit, regardless of what the actual value at such a point is. For a "real" example, with an actual function given by a formula and all, see below.
These conditions are very useful, but still too restrictive in some situations, for instance we cannot apply them to functions that involve the square root, with improper one-sided derivative at the origin. Another useful version of conditions uses piecewise monotonicity.
Theorem (Dirichlet).
Let f be aT-periodic function that is bounded and piecewise monotone. Denoteω = 2π/T. Let
Then for every t we have
This theorem could also be applied to the above picture. The difference is that now, when dividing the domain into intervals of monotonicity, we would have to split the intervals where the function has the shape of a hill, whereas the previous theorem could handle them whole.
Note that while for continuous functions we have uniform convergence (which
is definitely something desirable), there is no hope of having it when the
function has some discontinuities. To see what is happening, imagine a very
simple function with discontinuity, a function f that is identically
0 for x from
Partial sums of the corresponding Fourier series are trying to approximate
f well, and because f is continuous and continuously
differentiable on
Moreover, as a continuous functions, partial sums cannot jump from 0 to 1 at
once, but this jump takes some room (on the
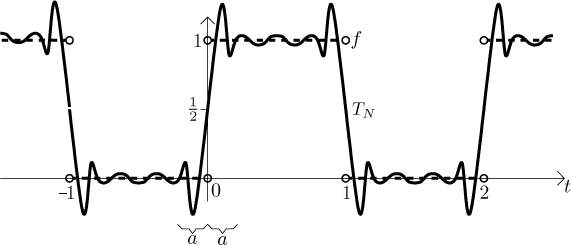
Note that we have uniform convergence on any closed interval that does not
include points of discontinuity. In particular, if we take any
As those partial sums shoot up really fast, they actually overshoot and go significantly higher than 1, only then they settle down. We can also read this situation right-to-left, those partial sums fall down really fast and overshoot also on the left. This behavior appears every time a Fourier series has to deal with discontinuity. On each side of it, partial sums exhibit oscillation that gets progressively narrower and narrower, but its size stays large. This disturbance is called the Gibbs phenomenon and you can see it in an actual example in this note.
We conclude this part with some simple observations. First and
importantly, since all functions involved are
Fact.
Let f be aT-periodic function for someT > 0, denoteω = 2π/T. Assume that f is Riemann integrable on an interval[a,a + T ] for some real number a. Then the coefficients of its Fourier series are given by
One popular choice is to integrate over the interval from
Proposition.
Let f be aT-periodic function that is integrable on some interval of lengthT > 0. Consider its corresponding Fourier series.
• If f is an odd function, then
• If f is an even function, then
In short, odd functions yield sine series and even functions yield cosine
series. We will make use of this later, see
sine and cosine Fourier series.
Functions on intervals
We just saw that to create a Fourier series we actually only need to know
the function f on some interval of the form
Definition.
Let f be a function that is defined on some interval of the form[a,a + T ). We define its periodic extension as the function f defined on the whole real line by the formula
Note that there is a little mix-up in that definition. The f on the right is the original f that is defined only on the given interval, while the f on the left is the new function defined on the real line. Since these two functions agree whenever they are both defined, it is customary to use one letter for both, although it may look a bit funny in this definition.
Now we can create a Fourier series also for functions that are given only on some finite interval.
Definition.
Let f be a function that is defined on some interval of the form[a,a + T ). Assume that it is Riemann integrable there. We define its Fourier series as the Fourier series of its periodic extension.
Note that we formally get a Fourier series defined on the whole real line, but since f was originally defined only on some interval I, we usually care only about what the series does there. However, as we will see below, in order to see this we do have to look also a bit around, at the periodic extension.
Example: We derive the Fourier series for the function
![]()
This function is continuous, hence integrable. When we extend it
periodically, we get a

We are ready to form the appropriate trigonometric series. In order to make
it look better we recall that
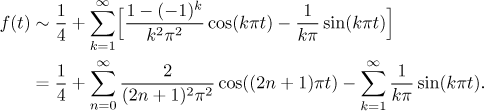
Now what does this series have to do with the given function f? We actually assigned this Fourier series to the periodic extension of the given f, so we should start by visualizing it (see the first graph in the picture below). Can we use the Jordan theorem to determine the convergence of our series? By looking at the picture we see that the periodic extension consists of segments where f is a straight line, so it is definitely continuous and differentiable on these pieces, with convergent limits (of f and f ′) at endpoints. After all, in the definition we have only formulas that are both continuous and continuously differentiable with limits at endpoints, which is something that cannot be spoiled by going to periodic extension.
Anyway, the Theorem above applies and thus the series behaves as follows.
The function f is continuous at all points of the interval
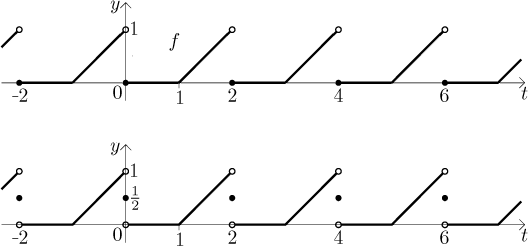
This is usually considered a sufficient answer to the following question: "What is the sum of the resulting Fourier series?" To see more details on convergence of Fourier series in this example, see this note. In particular you will see animation of partial sums and the Gibbs phenomenon.
One reason why the picture is usually considered sufficient is that writing
it down using formulas would be ugly and much less transparent. Just to show
you, we will do an exception and write the above result "properly", but only
for the interval

What are we to make of such a result? The basic idea is that we express the given function as a sum of various oscillations, a typical example might be a sound signal that is expressed as a combination of basic harmonic sounds. If a certain coefficient ak or bk is markedly larger than the others, then it means that this particular frequency is very prominent in the given signal. This can be used for "frequency analysis", but we talk more about it in the section on Applications.
In general, when we express the given function as Fourier series, it features both cosines and sines. Sometimes it would be useful if we could only use functions of our choice - either sines only or cosines only. In many cases there is a way to achieve this.
Recall that we proved earlier that odd functions have Fourier series without cosines and even functions have them without sines. This points to the way to do what we want. Of course, if we are given a function on the whole real line, then we have to rely on the symmetry it already has. However, if we are given a function just on an interval I of length L, then we can sometimes fix it so that its periodic extension becomes even or odd.
Consider a function defined on an interval of the form
The real trick lies in how we do the extension to
Definition.
Let f be a function defined and integrable on an interval[0,L ).
We define the sine Fourier series of f as the Fourier series of its odd periodic extension.
We define the cosine Fourier series of f as the Fourier series of its even periodic extension.
When we double the period, we also get a different frequency,
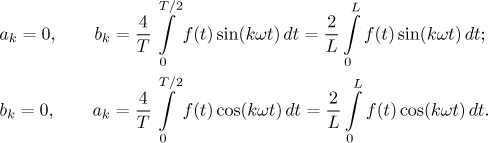
Surprisingly, apart from the different frequency the above formulas ended up exactly the same as if we were doing the usual Fourier series, just instead of T we use L. This is rather convenient.
Fact.
Let f be a function defined and integrable on an interval[0,L ).
The sine Fourier series of f is the trigonometric series withω = π/L and coefficients given by
The cosine Fourier series of f is the trigonometric series withω = π/L and coefficients given by
If f is piecewise continuous with piecewise continuous derivative on
Its cosine Fourier series converges to the even periodic extension of
f modified at discontinuities using averages.
Example: We return to the above example and find its sine and cosine
Fourier series. We have
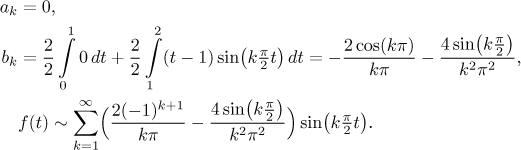
Now we derive the cosine Fourier series.

If we want to know to what function do these two Fourier series converge, we have to first make the odd and even periodic extensions of f and then apply the averaging trick to points of discontinuity. In the picture we emphasize the basic doubled period.

Note that the even periodic extension is actually a continuous function,
therefore the cosine Fourier series converges uniformly to it. When we
naturally focus on the interval
Properties of Fourier series
Back to Theory - Series of functions