Důležité příklady

V této části probereme základní příklady posloupností a podíváme se na jejich omezenost a monotonii. Začneme alternující posloupností, ke které se ještě vrátíme na konci, stručně probereme aritmetické posloupnosti, nejdůležitějším typem ale je geometrická posloupnost. K těmto příkladům se ještě vrátíme v části Teorie - Limita - Důležité příklady.

Alternující posloupnost

Alternující posloupnost je vlastně kategorie, obecnější typ posloupnosti (viz konec této části), ale zde se podíváme na posloupnost, která je jakýmsi prototypem alternující posloupnosti:

Graf vypadá takto:

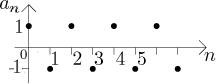
Z obrázku hned vidíme, že tato posloupnost je omezená (pro všechna n evidentně máme |(−1)ⁿ| ≤ 1) a není monotonní. Nemůže být rostoucí či neklesající, protože druhý člen (když n = 1) je menší než první člen (když n = 0), takže tam posloupnost klesne; nemůže také být klesající nebo nerostoucí, protože třetí člen je větší než druhý člen, neboli tam posloupnost vzroste.

Je také možné indexovat tuto posloupnost od n = 1. Jsou dva důvody pro začátek od nuly, jak jsme to zde udělali. První důvod je má preference - prostě se mi líbí víc, když posloupnost začne kladným číslem než číslem −1, a občas je to dokonce takto pohodlnější. Druhý důvod bude jasnější, když dojde řeč na geometrickou řadu.

Tato posloupnost se objevuje docela často; někdy sama o sobě, ale častěji jako součást jiné posloupnosti; viz poslední sekce níže.

Definice.
Aritmetickou posloupností rozumíme libovolnou posloupnost typu

a_n = a + nd, n = 0,1,2,3,...

kde a a d jsou libovolná pevně zvolená reálná čísla.

Aritmetická posloupnost tedy vypadá takto:

{a, a + d, a + 2d, a + 3d, a + 4d,...}.

Je zase možné indexovat tuto posloupnost n = 1,2,3,..., ale pak by bylo prvním členem posloupnosti číslo a+d, což není tak pěkné jako začínat s a.

Všimněte si následujícího: každý člen aritmetické posloupnosti lze získat přičtením konstanty d k předchozímu členu. Například

a₅ = a + 5d = (a + 4d) + d = a₄ + d.

To je základní myšlenka aritmetické posloupnosti. Začne se nějakým číslem a a pak se přičítá zas a zas stejný rozdíl d. Nemělo by tedy překvapit, že aritmetická posloupnost může být tedy definována rekurzivně takto:
(1)    a₀ = a,
(2)    a_n+1 = a_n + d, n = 0,1,2,3,...

Není těžké dokázat indukcí, že jak explicitní, tak rekurzivní definice definují tutéž posloupnost.

Poslední charakterizace aritmetické posloupnosti: Daná posloupnost je aritmetická právě tehdy, je-li rozdíl mezi dvěma následujícími členy stále stejný.

Příklad:
{2, 0.5, −1, −2.5, −4, −5.5,...} je aritmetická posloupnost. Opravdu, rozdíl mezi následujícími členy je vždy d = −1.5. Ověřte, že pro n = 0,1,2,3,.. jsou členy posloupnosti dány vzorcem a_n = 2 + (−1.5)n.

Zvolili jsme tento příklad, abychom ukázali, že krok d může také být záporný. Je jeden speciální případ, a to když d = 0. Pak a_n = a pro všechna n a dostaneme konstantní posloupnost {a, a, a,...}.

Jaké jsou vlastnosti aritmetické posloupnosti? Nejprve se podíváme na triviální případ konstantní posloupnosti a_n = a pro všechna n.

Hned vidíme, že taková posloupnost je omezená; navíc je monotonní, jmenovitě zároveň neklesající a nerostoucí.

Co se stane pro d nenulové? Jsou dva případy.

Případ 1: Jestliže d > 0, pak je posloupnost rostoucí (a také neklesající), neboť

a_n+1 = a_n + d > a_n.

Z odhadu a_n = a + nd > a také vidíme, že takováto posloupnost je omezená zdola. Na druhou stranu není omezená shora a tudíž není omezená.

Případ 2: Jestliže d < 0, pak je posloupnost klesající (a také nerostoucí), neboť

a_n+1 = a_n + d < a_n.

Z odhadu a_n = a + nd < a také vidíme, že takováto posloupnost je omezená shora. Na druhou stranu není omezená zdola (důkaz je podobný předchozímu případu), tudíž není ani omezená.

Definice.
Geometrickou posloupností rozumíme libovolnou posloupnost typu

a_n = aqⁿ, n = 0,1,2,3,...

kde a z q jsou pevně zvolená reálná čísla.

Geometrická posloupnost tedy vypadá takto (máme aq⁰ = a⋅1 = a):

{a, aq, aq², aq³, aq⁴,...}.

Je zase možné indexovat tuto posloupnost n = 1,2,3,..., pak by ale bylo jejím prvním členem číslo aq, což není tak pěkné jako začínat členem a. Ve většině případů máme dokonce a = 1, takže typická geometrická posloupnost vypadá takto:

{1, q, q², q³, q⁴,...}.

Jeden příklad geometrické posloupnosti jsme už viděli, jmenovitě onen prototyp alternující posloupnosti na začátku.

Všimněte si, že každý člen geometrické posloupnosti lze získat vynásobením předchozího členu konstantou q. Například

a₅ = aq⁵ = (aq⁴)q = a₄q.

To je základní myšlenka geometrické posloupnosti. Začnete nějakým číslem a pak jej zas a zas násobíte touže konstantou q. Nemělo by tedy překvapit, že geometrickou posloupnost lze také definovat rekurzivně takto:
(1)    a₀ = a,
(2)    a_n+1 = a_nq, n = 0,1,2,3,...

Není těžké dokázat indukcí, že jak explicitní, tak rekurzivní definice definují tutéž nekonečnou posloupnost.

Poslední charakterizace geometrické posloupnosti: Daná posloupnost je geometrická, pokud podíl dvou následujících členů je vždy stejný.

Ten příklad geometrické posloupnosti, který jsme viděli dříve (alternující posloupnost), je poněkud speciální, a tak není dobrým reprezentantem chování geometrické posloupnosti. Další výjimkou je případ, kdy a = q = 1. Dostaneme posloupnost {1, 1, 1, 1, 1,...}, což je konstantní posloupnost, na kterou se můžeme dívat také jako na aritmetickou posloupnost. Je mimochodem docela jednoduché dokázat algebraicky, že pokud je nějaká geometrická posloupnost konstantní, pak nutně q = 1 a tato posloupnost je také aritmetická. Na druhou stranu, jediné posloupnosti, které jsou zároveň aritmetické a geometrické, jsou konstantní posloupnosti. Na ně se samozřejmě vztahují příslušné závěry, jsou omezené a monotonní.
Abychom to shrnuli, případy q = −1 a q = 1 jsou speciální a kdykoliv dojde na geometrickou posloupnost (či geometrickou řadu), budou se chovat jinak než ty ostatní.

Abychom viděli, co se děje, když je q jiné, se podíváme na čtyři typické příklady, pro jednoduchost položíme (jako obvykle) a = 1.

Příklad:
Volba q = 2 dává posloupnost a_n = 2ⁿ, neboli

{2⁰, 2¹, 2², 2³, 2⁴,...} = {1, 2, 4, 8, 16, 32, 64,...}.

Tato posloupnost je rostoucí, omezená zdola (evidentně a_n > 0 pro všechna n) ale není omezená shora, tedy ani omezená.

Příklad:
Volba q = 1/2 dává posloupnost a_n = (1/2)ⁿ = 1/2ⁿ, neboli

{1/2⁰, 1/2¹, 1/2², 1/2³, 1/2⁴,...} = {1, 1/2, 1/4, 1/8, 1/16, 1/32, 1/64,...}.

Tato posloupnost je klesající, omezená zdola (evidentně a_n > 0 pro všechna n) ale také shora (a_n ≤ 1 pro všechna n = 0,1,2,3,...), tedy je omezená.

Tyto dva příklady ukazují dva základní typy geometrické posloupnosti, jmenovitě když q > 1 a když 0 < q < 1. V následujících dvou příkladech použijeme tatáž čísla, ale se záporným znaménkem, čímž získáme dva typické příklady pro záporná q: jmenovitě když q < −1 a −1 < q < 0. Protože pro záporná q můžeme psát q = (−1)|q|, uvidíte, že tyto dva případy budou vlastně založeny na předchozích dvou, které jsou jen modifikovány "přilepením znamének" alternující posloupnosti z prvního příkladu na začátku.

Příklad:
Volba q = −2 dává posloupnost a_n = (−2)ⁿ = (−1)ⁿ2ⁿ, neboli

{2⁰, −2¹, 2², −2³, 2⁴,...} = {1, −2, 4, −8, 16, −32, 64,...}.

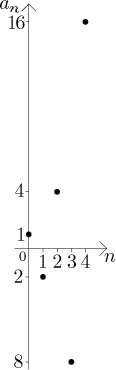
Tato posloupnost není monotonní, není omezená zdola ani shora, tedy ani omezená.

Příklad:
Volba q = −1/2 dává posloupnost a_n = (−1/2)ⁿ = (−1)ⁿ/2ⁿ, neboli

{1/2⁰, −1/2¹, 1/2², −1/2³, 1/2⁴,...} = {1, −1/2, 1/4, −1/8, 1/16, −1/32, 1/64,...}.

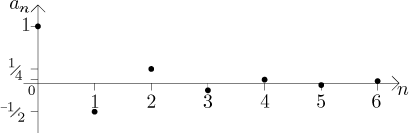
Tato posloupnost není monotonní, je omezená zdola (evidentně a_n > −1 pro všechna n) a také shora (a_n ≤ 1 pro všechna n = 0,1,2,3,...), tudíž omezená.

Pro další informaci viz Důležité příklady v části Posloupnosti - Teorie - Limita.

Všimněte si, že v těchto posledních dvou příkladech jsme vlastně vzali grafy předchozích dvou příkladů a přehodili každý druhý člen dolů okolo osy n. To naznačuje, že při zkoumání posloupností, jejichž znaménka se mění pravidelně, může být výhodné je nejprve ignorovat. To nás přivádí k poslednímu tématu.

Náš první příklad byl prototypem alternující posloupnosti. Teď se podíváme na obecnější definici.

Definice.
Alternující posloupností rozumíme libovolnou posloupnost {a_n}, kterou je možné zapsat jako a_n = (−1)ⁿb_n pro nějaká nezáporná reálná čísla b_n.

Mimochodem, spousta lidí by dala přednost začít indexování nějakým sudým číslem, aby daná alternující posloupnost začínala plusem; myslím, že řekněme {b₀, -b₁, b₂, -b₃,...} vypadá mnohem lépe. Ještě stažší je ovšem prostě prohlásit, že coby alternující posloupnosti uvažujeme i posloupnosti, jejichž členy lze zapsat jako a_n = (−1)ⁿ⁺¹b_n pro nějaká nezáporná reálná čísla b_n. Pro zjednodušení budeme formalně pracovat s typem z definice, ale vše samozřejmě funguje i pro tento druhý typ, který má znaménka přesně naopak.

Při vyšetřování alternující posloupnosti

{a₁, a₂, a₃,...} = {-b₁, b₂, -b₃,...}

je často jednodušší nejprve ignorovat znaménka a vyšetřovat posloupnost {b₁, b₂, b₃,...}, pak teprve vzít ta znaménka v úvahu - už proto, že mnohé metody se dají aplikovat pouze na posloupnosti s nezápornými členy, takže je možné je použít na onu posloupnost bez znamének, ale ne pro tu původní alternující. Ignorování znamének také může pomoci, pokud se snažíme využít vztahu mezi posloupnostmi a funkcemi (viz Posloupnosti a funkce v sekci Teorie - Limita).

Obzvláště při kreslení grafu alternující posloupnosti je obvykle jednodušší nejdříve vyšetřit tvar grafu {b_n}, pak přikreslit jeho zrcadlový obraz a nakonec nakreslit body alternující posloupnosti tak, že si střídavě vybíráme z horního a dolního tvaru:

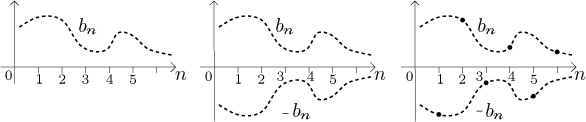
Všimněte si, že tuto ideu je také možné použít na kreslení grafu posloupností, jejichž znaménka se mění pravidelným způsobem, i když to není ten alternující. Například {1, 2, −4, 8, 16, −32, 64,...} je posloupnost (založena na našem geometrickém příkladě), která není alternující, přesto se znaménka mění pravidelně; v takových případech je často možné ignorovat mínusy, kde to přijde vhod, a pak je zase doplnit později.

Poslední poznámka: Existují i posloupnosti, jejichž znaménka nejen nealternují, ale dokonce ani nemají nějakou pravidelnost; jinými slovy, neexistuje určitý vzorec znamének, který by se dokola opakoval, a co je důležitější, ze znalosti určitého počtu členů nemůžeme odvodit, jaké znaménko má následující člen (tj. jen ze známých znamének, bez přímého výpočtu onoho členu ze vzorce). Asi nejjednodušší příklad je {sin(n)}, n = 0,1,2,3,... (jako obvykle, funkce sinus se bere v radiánech, ne ve stupních). Posloupnost jde {sin(1), sin(2), sin(3), sin(4),...}. První tři členy jsou kladné, ale protože 4 je větší než π a menší než 2π, je sin(4) záporný, stejně jako sin(5) a sin(6), sin(7) je kladný a tak dále. Dokázat, že žádná pravidelnost neexistuje, je dosti těžké, musíte mi věřit, ale jakýsi pocit můžete získat, když si spočítáte prvních řekněme 30 členů. Uvidíte, že znaménka přichází ve skupinách po třech či čtyřech, ale výskyt skupin po čtyřech není vůbec pravidelný.

Operace s posloupnostmi
Zpět na Teorie - Úvod