Důležité příklady

Zde se podíváme na nejdůležitější příklady posloupností. Soustředíme se na jejich konvergenci, zmíníme se také o omezenosti a monotonii posloupností, které tady uvidíme poprvé. Po alternující a aritmetické posloupnosti se podíváme na geometrickou posloupnost, pak se podíváme na mocniny, faktoriál, exponenciálu a nakonec na sinus a kosinus.

Alternující posloupnost

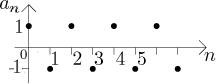
Jak už jsme viděli, prototyp alternující posloupnosti {(−1)ⁿ}_n=0,1,2,... je jen speciální případ geometrické posloupnosti (viz níže), ale je tak důležitý, že se na něj podíváme zvlášť.

Už z obrázku vidíme, že tato posloupnost nemá limitu. Toto je nejjednodušší příklad problému typu oscilace zabraňujícího existenci limity.

Aritmetická posloupnost

Chování aritmetické posloupnosti {a + nd}_n=0,1,2,... záleží na parametru d.

Jestliže d = 0, dostaneme konstantní posloupnost:

Z obrázku se zdá jasné, že tato posloupnost konverguje, a opravdu platí, že

Jestliže d > 0, máme tuto situaci:

Taková posloupnost je divergentní, ale limita existuje a je rovna nekonečnu; to jest, (a + nd)→∞. Důkaz jenaznačen u důkazu, že tato posloupnost není omezená shora.

Jestliže d < 0, máme tuto situaci:

Taková posloupnost je zase divergentní, ale má limitu, tentokráte mínus nekonečno; tedy (a + nd)→−∞.

Chování geometrické posloupnosti {qⁿ}_{n=0,1,2,3,...} záleží na parametru q. Za prvé, jestliže q = −1, dostaneme alternující posloupnost, jejíž limita neexistuje. Jestliže q = 1, dostaneme kontantní posloupnost {1, 1, 1,...}, která konverguje k 1 (viz konstantní aritmetická posloupnost výše).

Pro další případy je dobré si připomenout čtyři typické příklady, které jsme viděli v části Teorie - Úvod - Důležité příklady. Reprezentovaly čtyři alternativy, které se mohou stát pro |q| ≠ 1. Teď je použijeme k ukázání typického chování.

Případ 1: q > 1.

V tomto případě posloupnost diverguje, ale má limitu, jmenovitě nekonečno (viz konec poznámky zde).

Případ 2: |q| < 1. Ačkoliv zde existují dvě alternativy, když 0 < q < 1

a když −1 < q < 0,

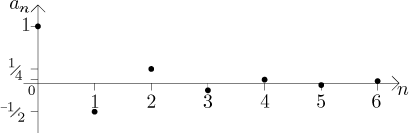
z pohledu konvergence je to tentýž případ: posloupnost konverguje k 0.

Případ 3: q < −1.

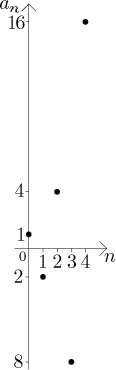
V tomto případě posloupnost nemá limitu. Všimněte si, že tento příklad kombinuje oba důvody divergence diskutované v úvodu k limitě: oscilaci a "vybouchnutí".

Fakta o geometrické posloupnosti lze shrnout několika způsoby. Z pohledu konvergence (a s vynecháním některých alternativ) máme pěkné a užitečné tvrzení:

Je také možné vyjádřit všechny detaily:

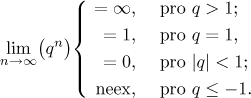
Ačkoliv je n ^a jeden typ výrazu, rozdělíme jej zde do dvou kategorií. Když se hledá limita, neboli když se hledá odpověď na otázku "co se stane danému výrazu, když se n stává velkým", je obvykle vyjádřit mocniny tak, aby byl exponent kladný. Takové výrazy hodně pomáhají naší intuici. Například místo psaní, řekněme, n⁻⁴, je lepší napsat 1/n⁴. Proto se nejprve podíváme na mocniny s kladnými exponenty a pak na mocniny se zápornými exponenty, které přirozeně napíšeme ve formě zlomku.

Případ 1: (mocnina v čitateli). Posloupnost {n ^a}_n=1,2,3,..., kde a > 0, je rostoucí, omezená zdola ale ne shora (tudíž není omezená). Několik typických příkladů:

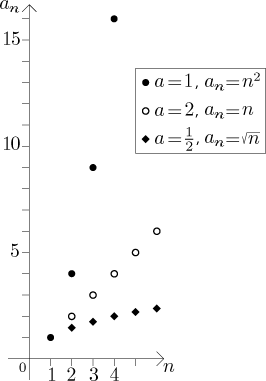
Máme následující fakt:

Případ 2: (mocnina ve jmenovateli). Posloupnost , kde a > 0, je klesající a omezená. Některé typické příklady:

Máme následující fakt:

Protože n! > n, intuice naznačuje, že posloupnost {n!}_n=1,2,3,..., která začíná {1, 2, 6, 24, 120, 720, 5040,...}, je rostoucí, omezená zdola ale ne omezená, a jde do nekonečna. Důkazy jsou snadné a ukážeme je:

Tato posloupnost je rostoucí, protože

a_n+1 = (n + 1)! = (n + 1)⋅n! = (n + 1)⋅a_n > a_n.

Limita plyne z jednostranného srovnání, viz sekce Limita a srovnání:

a_n = n! = n⋅(n − 1)! > n→∞.

Uvažujme posloupnost a_n = . Je snadné ukázat, že tato posloupnost je omezená shora. Pomocí triku se pak dá dokázat, že tato posloupnost je pro c > 0 rostoucí. Podle věty z následující části Základní vlastnosti je taková posloupnost konvergentní. Limita této posloupnosti je zrovna číslo e^c, to jest Eulerova konstanta umocněna na mocninu c. Tento závěr platí i pro záporná c, takže pro všechna reálná čísla c máme

Někteří lidé dokonce takto definují Eulerovo číslo. Řeknou, že Eulerovo číslo e = 2.718281828... je právě limita posloupnosti (1 + 1/n)ⁿ.

Posloupnosti {sin(n)} a {cos(n)} jsou dost důležité. Připomeňme si tvary těchto dvou funkcí:

Posloupnosti se pak vytvoří tak, že se místo x dosadí přirozená čísla, jinak řečeno, umístěním bodů do grafů na místa, kde jsou x-ové souřadnice celá čísla. Všechny vlastnosti teď záleží na tom, jak se tyto body, umístěné s rozestupem 1, shodnou s periodou sinu a kosinu, což je 2π. Jmenovitě, musíme se zeptat, zda se stane následující:

Platí pro tyto body nějaká providelnost, například takto?

Pravidelně nebo ne, může se stát, že body padnou na vlny takovým způsobem, že vzniklá posloupnost je monotonní?

Mohlo by se třeba stát, že se body začnou "vyhýbat" vrcholům a údolím, takže se posloupnost nakonec stane malá?

Mohly by body padnout na vlny tak, že posloupnost nakonec konverguje?

Všechny tyto otázky mají zápornou odpověď. Body padnou na vlny způsobem, který se stále mění a nikdy neopakuje, a nezačnou se vyhýbat žádné části sinové/kosinové vlny. Pokud si například vyberete určitou část základní vlny, pak ať už ignorujete jakkoliv velký začátek posloupnosti (sinové či kosinové, obě se chovají stejně), vždy se v konci najdou body, které padnou do této části, a když odříznete tuto část, zase se najdou body ve zbytku a tak dále. Následující obrázek ukazuje, jak to vypadá.

Co z toho plyne? Protože body mimo jiné znovu a znovu padnou na vrcholy a údolí, posloupnosti nemohou být monotonní. Budou se také znovu a znovu dostávat libovolně blízko k hodnotám 1 a −1, takže se velikost oscilace nezmění, přirozené meze 1 a −1 nelze vylepšit ignorováním nějakého začátku posloupnosti. Plyne z toho mimo jiné, že tyto posloupnosti jsou divergentní.

Pro podrobnější pohled na tuto problematiku klikněte sem.

Základní vlastnosti
Zpět na Teorie - Limita