Important examples

Here we will look at the most important examples of sequences. We will focus on their convergence, we will also remark on boundedness and monotonicity of sequences that are introduced for the first time here. After alternating and arithmetic sequences we look at geometric sequence, then we look at powers, factorial, the exponential, and finally sine and cosine.

Alternating sequence

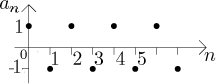
As we saw before, the prototype alternating sequence {(−1)ⁿ}_n=0,1,2,... is just a special case of a geometric sequence (see below), but it is such an important example that we will cover it separately.

Just by looking at the graph we see that this sequence does not have a limit. This is the simplest example of an oscillation-type problem preventing the existence of a limit.

Arithmetic sequence

The behaviour of the arithmetic sequence {a + nd}_n=0,1,2,... depends on the parameter d.

If d = 0, we get the constant sequence:

From the picture it seems clear that this sequence is convergent, and indeed we have

If d > 0, then we have this situation:

Such a sequence is divergent, but the limit exists and is equal to infinity; that is, (a + nd)→∞. The proof is outlined in the note on the proof that this sequence is not bounded from above.

If d < 0, then we have this situation:

Again, such a sequence is divergent, but the limit exists and is equal to negative infinity; that is, (a + nd)→−∞.

The behaviour of the geometric sequence {qⁿ}_{n=0,1,2,3,...} depends on the parameter q. First, if q = −1, we get the alternating sequence above whose limit DNE. If q = 1, we get the constant sequence {1, 1, 1,...} that converges to 1 (see the constant arithmetic sequence above).

For other values it is good to recall the four examples that we saw in Theory - Introduction - Important examples. They represented four alternatives that can happen if |q| ≠ 1. We will use them here to show the typical behaviour.

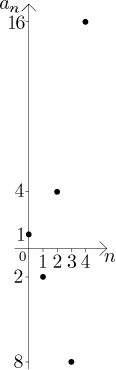
Case 1: q > 1.

In this case the sequence diverges, but has a limit, namely infinity (see the end of the note here).

Case 2: |q| < 1. Although there are actually two alternatives, when 0 < q < 1

and when −1 < q < 0,

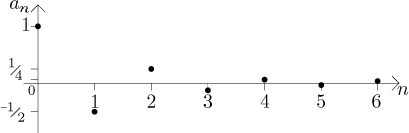
from the point of view of convergence it is the same case: the sequence converges to 0.

Case 3: q < −1.

In this case the sequence does not have a limit. Note that here the divergence combines both factors that we discussed in introduction to limits: oscillation and "blowing up".

The facts about geometric sequence can be summed up in several ways. From the point of view of convergence (and not covering all alternatives) one has a nice and handy statement:

It is also possible to express all the details:

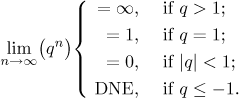
Although n ^a is just one type of expression, we will actually split it into two cases. When dealing with limits, that is, when trying to find answer to the question "what happens to a given expression when n gets really large", it is usually best to express powers so that the exponents have positive signs. Such expressions help our intuition a lot. In particular, instead of writing, say, n⁻⁴ it is better to write 1/n⁴. Therefore we will first look at powers with positive exponents and then at powers with negative exponents, they will be written naturally in the fraction form.

Case 1: (power in the numerator). The sequence {n ^a}_n=1,2,3,..., where a > 0, is an increasing sequence, bounded from below but not bounded from above (hence not bounded). Some typical examples:

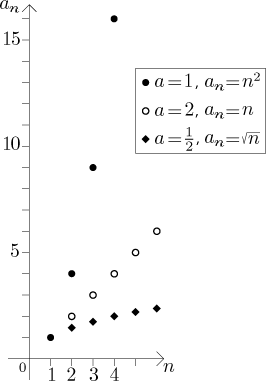
We have the following fact:

Case 2: (power in the denominator). The sequence , where a > 0, is a decreasing sequence that is bounded. Some typical examples:

We have the following fact:

Since n! > n, our intuition suggests that the sequence {n!}_n=1,2,3,... which goes {1, 2, 6, 24, 120, 720, 5040,...} is increasing, bounded from below but not bounded, and goes to infinity. Proofs are simple and we show them:

This sequence is increasing, since

a_n+1 = (n + 1)! = (n + 1)⋅n! = (n + 1)⋅a_n > a_n.

The limit follows by one-sided comparison, see the section Limit and comparison:

a_n = n! = n⋅(n − 1)! > n→∞.

Consider the sequence a_n = . It is easy to show that this sequence is bounded from above. It needs a trick to show that this sequence is also increasing if c > 0. By a theorem found in the next section Basic properties, such a sequence must be convergent. The limit of this sequence happens to be the number e^c, that is, the Euler number raised to the power c. This is true also for negative c's, so for all real numbers c we have

Some people actually define the Euler number this way. They would say that the Euler number e = 2.718281828... is exactly the limit of the sequence (1 + 1/n)ⁿ.

The sequences {sin(n)} and {cos(n)} are quite important. Recall the basic shapes of these two functions.

The sequences are created by substituting natural numbers for x; that is, by placing dots in these graphs at places where the x-coordinates are positive integers. All properties now depend on how the dots, spaced one-apart, fit with the period of sine and cosine, which is 2π. Namely, we have to ask whether the following things could happen:

Is there any pattern to the dots, for instance like this?

Pattern or no, could it happen that the dots hit the waves in such a way that eventually one has monotonicity?

Could it perhaps happen that the dots start "avoiding" hills and pits, so that the sequence eventually gets small?

Could the dots hit the waves in such a way that the sequence actually converges?

The answer to all these questions is negative. The dots hit the waves in ever changing ways that never repeat, and they do not start avoiding any areas of the sine/cosine waves. For instance, if you pick any part of the basic wave, then no matter how large a beginning of the sequence you ignore, in the remaining part of the sequence (both sine and cosine, they behave the same), the dots will again visit this segment, and if you cut this part of, then the sequence visits it again and so on. The following picture shows how the situation looks like:

What is the consequence? Since the dots in particular keep hitting hills and pits, the sequences cannot be monotone. They will also keep getting arbitrarily close to 1 and −1, so the magnitude of their oscillation does not change, the obvious bounds 1 and −1 cannot be improved by ignoring some beginning of the sequences. In particular, it should be clear that these sequences are divergent.

For more insight into this click here.

Basic properties
Back to Theory - Limits