In this section we will look closer at various properties of real numbers. Most of them have something to do with things happening close to or far from a certain point, and things of this sort are studied as topology in mathematics. Then we look at sets and ordering.
One of the most important properties of the real line is the fact that it "does not have holes" (see Real numbers in Extra - Sets and mappings - Important sets of numbers). We start with one possible way of expressing this fact.
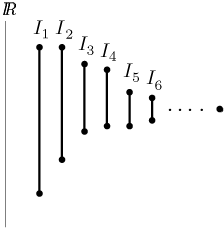
Theorem (Principle of nested intervals)
Let Ik for k natural numbers be closed intervals of real numbers. If these intervals are nested, that is, ifIk+1 ⊆ Ik for every k, then the intersection of all Ik is not empty.
If moreover the lengths of these intervals tend to zero, then their intersection is a single point.

Intersecting infinitely many sets is often tricky, this principle shows that
at least in the case of nested closed intervals we need not worry. Note that
closedness of these intervals is really crucial, otherwise the intersection
may be empty. For instance, if we intersect intervals
As we hinted above, this principle is another formulation of the completeness of real numbers. In the world of rational numbers this principle no longer works, it is easy to come up with a nested collection of closed intervals of rational numbers that has empty intersection. We will return to these consideration twice more times below.
Example: Consider the set
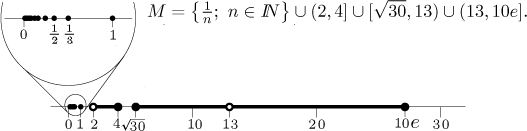
The point
The point
Now consider the point
Now we will look at another question. If we take a point a, how near
to it does M get? This question makes sense for both point from
M and points not from M. For instance, the points 5 and 13 are
not in M, but they differ in the following way. The set M gets
arbitrarily close to 13 (in other words, you can "get to 13" using points
from M), but for 5 this is not true, the nearest we get to 5 with the
set M is root of 30. We see similar difference when we look at points
4 and 1 from the set M. While we can get arbitrarily close to 4 using
other points of M, the point 1 is far from the rest of the set
M (the nearest point in M is
How do we express it mathematically? We want the definitions work for points that are in and also not in the set, in other words, when we ask "how near the set is to a certain point", we do not want the point itself to interfere. This can be easily done by using reduced neighborhoods. A point is isolated if it has a reduced neighborhood that is disjoint with M. Check that this fits with the examples above, it works for 1 and 5 but not for 4 and 13.
The fact that a set accumulates at some point can be expressed as follows:
Every reduced neighborhood of this point (no matter how small) has a
non-empty intersection with M. Now this is true for points 4 and 13.
Note that this definition is satisfied also for
Before we already mentioned the border of this set, we had a feeling that 1
and 4 are on the border (and intuitively 2 should be on the border as well).
How would we express the feeling that a point is on
the border mathematically (then we call it a boundary)? This is not so clear.
One possible requirement would be that the set exists on one side and does not
on the other, but although not "wrong", this definition turns out not to be
very useful, since border defined in such a way does not fit well with other
notions. Therefore mathematicians prefer a different definition, a
definition under which also the point 0 would be a boundary, since in a sense
the set ends there; it should also have the isolated points like 1 as
boundary. The idea is like this: M should get arbitrarily close to
such a point (but this time the point itself might help), but also the
outside of M should get arbitrarily close to such a point (and again,
the point itself may help, this makes sure that
Why such a long example? First, hopefully now we see how neighborhoods are used. If we want to have some freedom of movement without jumping out of a "nice" place, we would say "there exists some neighborhood where things are nice". If we want to say that a point cannot separate itself from something, we say "for every neighborhood something happens". These are the two most typical uses of neighborhoods and one sees a lot of this when working with functions (at least when working on them theoretically). The second reason is that we actually introduced informally some very useful notions and the following definition should make sense.
Definition.
Consider a subset M of real numbers and a point a.
We say that a is an interior point of M if there exists a neighborhood U of a such that U is a subset of M.
We say that a is an isolated point of M if there exists a reduced neighborhood P of a that is disjoint with M.
We say that a is an accumulation point or a cluster point of M if for every reduced neighborhood P of a the intersection of P with M is not empty.
We say that a is a boundary point of M if for every neighborhood U of a, the intersection of U with M is not empty and the intersection of U with M c is not emptyConsider a subset M of real numbers.
We define the interior of M, denoted Int(M ) or M o, as the set of all interior points of M.
We define the closure of M, denoted, as the union of M and the set of all its accumulation points.
We define the boundary of M, denoted ∂M, as the set of all boundary points of M.We say that the set M is open if it is equal to its interior (that is, if every its point is an interior point).
We say that the set M is closed if it is equal to its closure (that is, if all its accumulation points also belong to it).
Intuitively, a closed set is a set where if you start jumping around using its points, then you can never reach a place that is outside of it. To clarify these notions we return to the above example.
Interior points are all the points of the three intervals that are not at their ends, so the interior of this set is
Isolated points are those of the form
If we add the accumulation points above to M, we get the closure
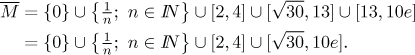
Since M is not equal to its interior nor to its closure, this set is not open nor closed. The boundary of M is
![]()
Note that if we add the boundary to the interior, we obtain the closure. This is a general fact, in general situations we define the boundary as
![]()
Note also that an open interval is an open set, this is actually the reason
why it is called this way. Closed interval is a closed set, note also that
the interior of an interval (of any kind) is the open interval with the same
endpoints, while the closure of any interval is the closed interval with the
same endpoints. Note that an interval
One can show that the interior of any set is an open set (if non-empty), while the closure of any set is a closed set. Open and closed sets play important role when working with functions.
We now return shortly to the notion of accumulation point. In the definition we require that every reduced neighborhood contains some point from M, but once we have this, then we can conclude that in fact every neighorhood of an accumulation point contains even infinitely many points from M. From this it immediately follows that finite sets cannot have accumulation points. How about infinite sets? Note that the set of integers does not have any acumulation point, so also here the situation is not quite clear. However, it can be shown that finiteness of the given set or the fact that it "runs away" are the only two ways to avoid concentration of points somewhere.
Theorem (Bolzano-Weierstrass theorem).
Every bounded and infinite subset of real numbers has an accumulation point.
Remarkably, this theorem is easy to prove using the Principle of nested intervals, and in turn this theorem can be used to prove that Principle. In other words, this is an equivalent way of expressing the fact that real numbers form a complete set. In particular, we cannot rely on existence of accumulation points in the world of rational numbers. This theorem has other versions (for instance one about a convergent subsequence, see the section Basic properties in Sequences - Theory - Limit), several important theorems also rely on this property, for instance the Extreme value theorem in the section Continuity in Theory - Real functions.
One more example of the use of topology.
Definition.
Let M be a subset of real numbers. We say that M is dense in ℝ if for every real number a and every reduced neighborhood P of a the intersection of P and M is not empty.
This definition is a bit pedestrian, it can be said in a more elegant way as follows: A set is dense if its closure is ℝ. Our definition is a bit more descriptive, intuitively a set is dense if we can approximate any real number with arbitrary precision using numbers from that set.
Rational numbers are dense in ℝ is a statement that should be obvious. What is more interesting is the fact that even quite small parts of rationals are still dense. For instance, consider the set
This set is rather smaller, we restrict ourselves only to fractions with denominators of the form 2n, but still this set is dense in ℝ. Facts like this can be quite useful in applications when we want arbitrarily good approximations but prefer to have small sets for it, for instance when we need to store information in computers.
Rather advanced remark for the curious, before we pass to another topic. We defined open sets in terms of interior, which in turn was defined using the notion of neighborhood. It turns out that one can also go the other way. If we decide which sets are open, then we get the same neighborhoods; not the same as sets, but the same concerning results that can be achieved using them. And achieve we can a lot. Using neighborhoods we define limits, and if we have functions on that space, we use neighborhoods to define derivatives. By a topology of a space we mean some description of what sets are open, or some description of what it means to be in a neighborhood of a point. A common way of doing this is to define some sort of a distance, then the neighborhoods work as we have them here, but one can also have neighborhoods without distance. Topological spaces (spaces where we have open sets and neighborhoods) have limits and lots of things we do with real functions here, it is a very abstract theory. However, if you understand the main idea of what was done here, you have a good chance to have at least a feeling about what can be done in general. It also explains why topology appears in the title of this section.
If we have a set with some ordering, we can ask some good questions about its subsets.
Definition.
Consider a subset M of real numbers. Let a be a real number.
We say that a is a lower bound for M ifa ≤ m for every m from M.
We say that a is an upper bound for M ifa ≥ m for every m from M.
We say that M is bounded (from) below if it has some lower bound.
We say that M is bounded (from) above if it has some upper bound.
We say that M is bounded if it is bounded above and below.
Consider the set M from the example above. It is bounded above, for
instance
![]()
On the other hand, the set of natural numbers (as a subset of the reals) is bounded from below (for instance by zero) but not from above, hence not bounded. Indeed, there is no real number x so that all natural numbers would be below it. The set of integers is not bounded in any sense.
When we have a set, it is sometimes useful to know where it "starts" and "ends".
Definition.
Consider a subset M of real numbers. Let a be a real number.
We say that a is the least number of M, or the smallest number of M, or the minimum of M, denoteda = min(M ), if it is a lower bound and belongs to M.
We say that a is the greatest number of M, or the largest number of M, or the maximum of M, denoteda = max(M ), if it is an upper bound and belongs to M.
In other words, a minimum is a number that lies in the given set and all other
numbers from the set are greater. For instance, the minimum of the set of
natural numbers in 1, but the set of integers does not have a minimum. Also,
the number 3 is the minimum of the set
Definition.
Consider a subset M of real numbers.
If M is bounded above, we define its supremum, denotedsup(M ), as the least upper bound. If M is not bounded above, we definesup(M ) = ∞.
If M is bounded below, we define its infimum, denotedinf(M ), as the greatest lower bound. If M is not bounded below, we defineinf(M ) = −∞.
Supremum and infimum are the right notions to tell us where a set begins and
ends. One can show that if a set has a maximum, then this maximum is also the
supremum of the set, similarly it works for minimum and infimum. If a set
does not have a maximum, then either the set is not bounded above, in which
case the set somehow extends to infinity and
There is a way to visualize these two notions. We look at
infimum first. If a set is not bounded below, then it extends somehow all the
way to the left and
![]()
The main advantage of supremum and infimum is this.
Theorem.
Every subset of real numbers has a supremum and an infimum and they are unique,
Note that the existence of supremum and infimum can be deduced from the Principle of nested intervals above, and also conversely the Principle follows from the existence of supremum and infimum. Thus this is another incarnation of the fact that real numbers are complete, in other words in the world of rational numbers we need not have supremum and infimum.
Supremum and infimum are in a sense limit notions, which is shown nicely in
their alternative definition. This definition is less elegant, but more
descriptive. Consider a set M and a number a. This number is
the supremum of M if
a) for every x from M we have
b) for every neighborhood U of a the intersection of U
with M is not empty.
Infimum is defined in analogous way. This definition has the advantage that it also works for infinite supremum/infimum in case of an unbounded set. When we recall the definitions of inequality and neighborhoods with infinity (see the previous section), we can also apply that new definition of supremum to a equal to infinity and we see that it works exactly as the original definition. Indeed, any real number is less than infinity, so infinity always satisfies the condition a). If also condition b) is satisfied, then the set is not bounded above and by the first definition, infinity is supremum of that set. If condition b) is not true for infinity, then the set is bounded above and some real number is its supremum.