Intervals and neighborhoods, extended real line

In this section we introduce basic tools for working on the real line and the extended real line.

In analysis we often talk about things being close. The key notion when talking about closeness is the distance. On a real line we use the usual distance, when the distance between points a and b is given by |a − b|. Note that the inequality |a − b| > 0 is equivalent to saying that a and b are not equal. We will use this soon.

Definition.
Consider real numbers a < b. We define
open interval     (a,b) = {x∈ℝ; a < x < b},
closed interval     [a,b] = {x∈ℝ; a ≤ x ≤ b},
half-closed interval (or half-open interval)     [a,b) = {x∈ℝ; a ≤ x < b},
half-closed interval (or half-open interval)     (a,b] = {x∈ℝ; a < x ≤ b}.

We also define
open interval     (a,∞) = {x∈ℝ; a < x},
open interval     (−∞,b) = {x∈ℝ; x < b},
closed interval     [a,∞) = {x∈ℝ; a ≤ x},
closed interval     (−∞,b] = {x∈ℝ; x ≤ b},

The points a, b are called endpoints of these intervals, we talk of intervals from a to b. In the last four cases also the infinity or negative infinity is considered an endpoint.

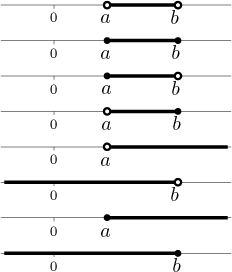
To have a better idea of properties of points and sets we usually draw them on a real line. For intervals we use filled dots for closed endpoints and empty circles for open endpoints. In the same order as in the definition:

Intervals are very popular, since they have many useful properties. Probably the most important property is that they are connected sets, that is, if we have two points from an interval I, then we can pass from one to another without ever getting out of I. In fact, every connected subset of a real line is an interval. We will see in the next part where the open/closed terminology came from. We will also see that those intervals with infinity are in fact nothing special, but for that we will have to extend real numbers. By the way, talking about infinity, the set of all real numbers is also an interval, namely (−∞,∞).

There are two kinds of rather funny intervals that are not exactly welcome in many applications, namely for any a we have (a,a) = {} and [a,a] = {a}. Analogous half-closed intervals are also empty. These empty and one-point intervals are called degenerate, all the other intervals are called non-degenerate. In many applications we only want to work with non-degenerate intervals, since these have non-empty interior (see the next section).

Intervals are important because many methods we will use only work on intervals, so they are, in a sense, our workplace. Now we will introduce another kind of a set which will be our working tool in analysis.

The difference is that a neigborhood contains its reference point a, while a reduced neighborhood does not. These neighborhoods can be also expressed using intervals, for instance

U_ε(a) = (a − ε,a + ε);       P_ε(a) = (a − ε,a) ∪ (a,a + ε).

We use neighborhoods to express some important ideas. In many situations we need to know what is happening just next to a given point, and this is best expressed using neighborhoods, as we will see below. Sometimes we do not care what happens on both sides of a, but we only worry about one side. For that we use one-sided neighborhoods.

Definition.
Consider a real number a and some ε > 0.
We define the right ε-neighborhood of a as

U_ε⁺(a) = [a,a + ε).

We define the left ε-neighborhood of a as

U_ε^-(a) = (a − ε,a].

We define the right reduced ε-neighborhood of a as

P_ε⁺(a) = (a,a + ε).

We define the left reduced ε-neighborhood of a as

P_ε^-(a) = (a − ε,a).

For instance, the left neighborhood looks like this:

In some situations it pays off to treat infinity as just another object. For instance, when we ask about a limit at some particular number a and about a limit at infinity, it turns out that the procedures used in answering such questions are basically the same. Thus it saves time if we can talk of some a, which can be a real number but also infinity, or perhaps negative infinity as the two "ends" of the real line.

We therefore introduce the extended real line (denoted ℝ^*) as the real line plus two abstract elements ∞ and −∞. Points of this set now fall into two categories, real numbers are proper points and the two elements ±∞ are improper points.

In order to be able to work with extended reals we need to extend also the operations and ordering. We define that for every real number a we have −∞ < a < ∞. We also put |−∞| = ∞. Concerning operations the situation is a bit delicate. We have to define them in such a way that they make sense and fit fell with operations we already have. We naturally arrive at the following:

• Addition: ∞ + ∞ = ∞, ∞ + a = ∞ for any real a, ∞ − a = ∞ for any real a, −∞ + a = −∞ for any real a, −∞ − a = −∞ for any real a.
• Multiplication: ∞ ⋅ ∞ = ∞, ∞ ⋅ a = ∞ for any real a > 0 and ∞ ⋅ a = −∞ for any real a < 0, −∞ ⋅ a = −∞ for any real a > 0 and −∞ ⋅ a = ∞ for any real a < 0, ∞ / a = ∞ for any real a > 0 and ∞ / a = −∞ for any real a < 0, −∞ / a = −∞ for any real a > 0 and −∞ / a = ∞ for any real a < 0. We also set −∞ = (−1) ⋅ ∞.
• ∞^a = ∞ for any a > 0, ∞^a = 0 for any a < 0, a^∞ = ∞ for any real a > 1, a^∞ = 0 for any a satisfying |a| < 1.

Note that some operations are not listed, for instance ∞ − ∞, 0 ⋅ ∞, ∞ / ∞, 1^∞ etc. These operations cannot be defined to make sense, this will be seen when working with limits (see for instance the note on indeterminate expressions).

To take the advantage of extended real numbers requires that we also generalize the notions that we had above. First, note that in the definition of intervals we listed four separate cases with infinite endpoints, but now that we have extended real numbers they are not needed. We can simply use appropriate definitions from among the first four and apply them also to cases when one or both endpoints are improper. Note however that the infinities themselves are never elements of intervals (intervals only include real numbers), in other words, we never close intervals at their improper endpoints.

The next important notion is neighborhood and there we will have to do some extra work. What do we expect of neighborhoods? They are sets that are connected and extend to the left and to the right of the given point a. With infinities this is not possible, since we can go to only one side, so we will have to make a modification here. In fact, for neighborhoods of improper points the both-sided and one-sided notions of neighborhood coincide, we do not have much choice there. Also, the distinction between neighborhoods and reduced neighborhoods becomes irrelevant, since a neighborhood of infinity (or minus infinity) will contain only real numbers and therefore they are automatically reduced.

Finally, a neighborhood of a proper point is given by a parameter ε that says how far one can go from the given point. This does not help us when a is improper, since every real number is infinitely far from infinity. Therefore we use another point of view at neighborhoods of proper points. If we take all possible neighborhoods of a proper point a and let ε go to zero (from the right, since ε can only be positive), then the ends of neighborhoods go to the center a. And this is something that we can emulate for neighborhoods of infinity and negative infinity. Now we are ready to understand the following definition.

Definition.
Consider ε > 0.
We define the ε-neighborhood of ∞ as

U_ε(∞) = (1/ε,∞).

We define the ε-neighborhood of −∞ as

U_ε(−∞) = (−∞,−1/ε).

Now we can work with neighborhoods and we do not really care whether the reference point a is proper or improper.

Once we can use infinity as a point, many definitions that would have to be done twice can be done just once. For a simple example see supremum at the end of the next section, a big simplification appears in the definition of the limit, see Definition of a limit in Functions - Theory - Limit of a function.

Topologic notions
Back to Theory - Real numbers