Real functions are the most important type of a mapping. After introducing this notion we look at inverse functions and functions defined by cases.
Definition.
By a real function of real variable we mean any mapping from some subset of the set of real numbers to the set of real numbers.
Note that people usually say just real functions and it is understood that we mean real functions of real variable. Other kinds of real functions (like real functions of complex variable) are always specified in full.
To a matematician, this definition of real functions is entirely satisfactory, since all properties known for mappings readily transfer to functions. However, for a practical user of mathematics this is less suitable, since one can happily and efficiently use real functions without even knowing about the existence of general mappings, and one can also do with less precision. We will therefore try to explain what a real function is without referring to mappings. This is best done by means of an example. We will use one inspired by physics, since indeed physics has been the inspiration for introducing functions in the first place. We will also use this example to review notions of domain, 1-1, onto, and inverse, so we definitely recommend that you look at it. We prefer to offer it as a separate page, since it is quite long and also since we will refer to it in other parts of Math Tutor.
Now we will briefly cover the basic notions.
A real function is a prescription which assignes values to arguments. The
notation
There is an alternative way to express the idea hat we substitute some concrete number into a function. It uses a slightly lowered vertical bar and goes like this:
![]()
This notation is especially handy if the function is not ripe for substituting yet and we want to make some adjustments first. For example,
![]()
The best way to visualize functions is by means of the graph, where we
mark in the two-dimensional plane

Note that if a function is given by a formula, we may be also interested in its algebraic make-up, which is another way to look at it, independent of the geometric point of view of the graph. For detail see the note on order of evaluation.
The domain of the function is sometimes given when the function is
defined. More often, the real function is just given as a prescription, a
formula, in which case for domain we take the set of all numbers x that
can be substituted into the function, that is, for which the formula defining
the function makes sense. It is usually denoted by
Typically, the domain would be a union of intervals.
The range of the function is the set of all values that can be
obtained by substituting arguments from the domain. It is usually denoted by
Sometimes the given function is considered only on a subset of the domain. We
then say that the function was restricted to this subset, the new
function is called the restriction. If M is a subset of the
domain

The restricted function has a different domain and might have a different range (although this is not necessary, sometimes a function can cover all its values on that subset to which we restrict it and only repeats them in the parts that were ignored).
The properties of functions depend a lot on their domains, so one in fact always has to think of a function and its domain as a pair. This is also reflected in the following
Definition.
We say that two functions, f and g, are equal, denotedf = g, if they have the same domain D and for all x from D we havef (x) = g(x).
Consider the following example. This equality is obviously true:
![]()
Now we will define two functions.
![]()
Although algebraically these two formulas are the same, the two functions are not, we cannot write f = g, because their domains are not the same:
![]()
Sometimes we want to disregard values of f outside a specific set M, but we still want to be able to work on its whole domain. Then the notion of restriction does not help, instead we can "kill" the values of f outside M like this:
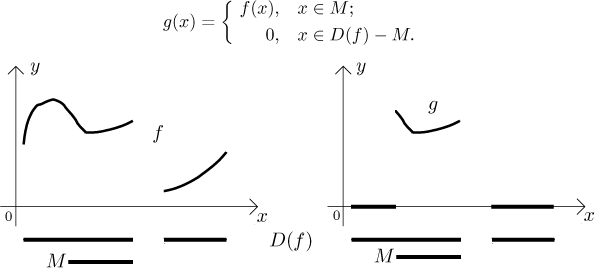
This approach has several advantages, one is that the function g can be expressed algebraically, see the section on characteristic functions in Theory - Elementary functions.
There is an alternative way to visualize functions. It carries less actual information about the given function, but it is sometimes helpful in emphasizing the function as a procedure for sending points from one set to points in another set. A real function actually sends points from one copy of reals to another (different) copy of reals, the difference is emphasized by different letters for elements of the two sets.
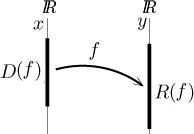
Sometimes we may even indicate how some points are sent, for instance the
function

1-1 functions.
A function is said to be 1-1 if it does not happen that
two different arguments would lead to the same value. That is, for a 1-1 function
f it cannot happen that for distinct

In practice it is easier to work with a different condition, formally the counterpositive of the above conditon: If after substituting two points we get the same value, then it must have been the same point.
Definition.
We say that a function f is 1-1 (or injective, or an injection) if for allx1,x2 from its domain the following implication is true: Iff (x1) = f (x2), thenx1 = x2.
If we were also given a target set B with the function f, we
can ask whether f is onto (or surjective, or a
surjection), that is,
whether the target set is equal to the range,
A function is bijective (a bijection) if it is 1-1 and onto. For real functions this means that we only worry about being 1-1.
By an inverse function of a function f (or its inverse
for short) we mean another function g
which satisfies the condition
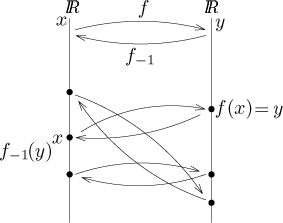
If such an inverse function exists, we denote it
There is a well-known theorem which states that an inverse exists exactly when the given function is a bijection. For real functions we however have a special form:
Theorem.
Assume that f is a real function with domainD( f ) and rangeR( f ). It has an inverse if an only if it is1-1. Then the inverse is unique and satisfies
D( f−1) = R( f ), R( f−1) = D( f ).
The graph of an inverse function can be obtained by flipping the graph of f around the main diagonal. This, by the way, shows the importance of being 1-1 for the existence of an inverse. In the following picture we first show an example of a function that has an inverse. The second picture shows a function that is not 1-1 (we get to the indicated value y from two different values of argument). You can see that when we attempt to flip around its graph, we obtain something that is definitely not a graph of a function, since a function cannot have two values for one argument.
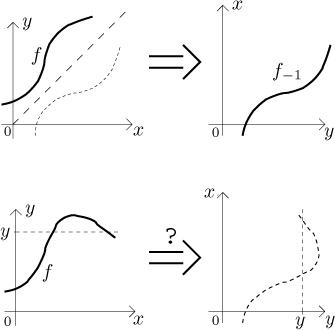
We will return to the inverse in the next section, Operations with real functions, namely when talking about composition.
Example. Consider the function
First we need to look at the domain. What numbers x can be substituted
into this formula? We know that any real number can be squared, so the answer
is: All real numbers. Therefore
Range is usually much less important, it is also often difficult to
determine, so in most cases we do not bother. However, here it is quite
simple, so we try it. What values can be obtained using the formula for
f ? We know from experience that squares are always positive or at
least zero, so the formula
What about being 1-1 and having an inverse? We know that these two questions
are equivalent. To solve the first one, we try to prove the implication for the definition.
We assume that
We know that this equation has two possible solutions. One is
We confirmed that two different arguments, 0 and 2, are assigned the same
value, namely 3. Therefore the function f is not
We can also try to find the inverse function and see if we succeed. For the
inverse to exist, we should be able to reverse the assignment
We know that this equation has two distinct solutions, namely we can have
x equal to 1 minus root of
Drawing a graph properly is covered later in Graphing functions in Derivative - Theory, so to get at least some idea of the graph of our f, we start by getting some points on it, that is, by calculating the values of f at many values of x. Of course, the more the better, but for simplicity we will try just some here:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
We put these values in the graph:
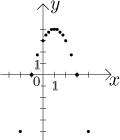
They suggest the general shape. In fact, the exact shape is a parabola turned down, like this:
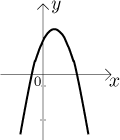
We see right away that this function is definitely not
We can also see from the picture that if we restrict this function to just
one branch of the parabola (or even just a part of it), it becomes

This function is now 1-1 and has an inverse, we confirm this by succesfully
finding it. We need to solve the equation
![]()
Thus we found the inverse function, incidentally proving that it exists and
that the function g is
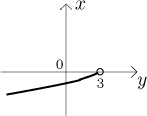
Note how it came naturally that the inverse function has y as its
variable. Since in most cases we prefer x as variable, people often,
when finding the inverse function, switch variables and eventually write
Note that if we chose another restriction on the left half of the parabola,
for instance to
Remark:
When talking about the inverse
One has to be a bit careful if there are more letters in play, say a function
may have its definition dependent on some parameter p. For instance,
the formula
Some functions are not given by just one formula, but by several, some arguments are being substituted into one formula, others into a different one. We say that such a function is defined "by cases", or that it is "piecewise-defined", or that it is a "split function" (which we prefer here), and typical example would be this:
![]()
How does this work? Arguments for which we know f can be taken from
the closed interval
When we want to substitute some x from the domain, we check into which
of the alternatives it falls and then use the appropriate formula. For
instance,
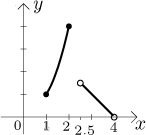
And that is exactly how functions defined by cases are investigated. Each case is checked separately and the graphs and answers are then put together. One can also have more cases with more interesting conditions, for instance the function
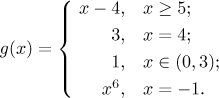
It has domain
and the graph
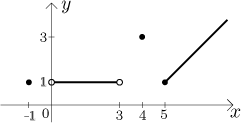
Some values:
This idea of putting together pieces of functions is used not only with
functions defined by cases, but also with functions that are defined by one
formula, but their domains split into several parts. For instance, the
function
Sometimes a function is given by one formula, but definition by cases is hidden in it, which is above all the case of the absolute value.
For more information on working with split functions see Split functions in Derivative - Theory - Graphing functions.
Operations with real functions
Back to Theory - Real
functions