Symmetry of a real function: Survey of methods
How do we determine whether a function f is even, odd or not
symmetric at all? There is a very simple algorithm using the definition.
1. First we look at the domain
D( f ). If this
set is not symmetric with respect to the origin, then the function f
cannot be symmetric either. For instance, the function
f (x) = ln(x + 3) has domain
D( f ) = (−3,∞), which is not symmetric
about 0. Thus f cannot be symmetric. On the other hand, the function
g(x) = arcsin(x2) + 1/x
has domain D(g) = [−1,0) ∪ (0,1],
which is a set symmetric about the origin and
therefore this function might concievably be symmetric.
2. If the domain is a symmetric set, we do the main test. We
substitute -x (a general point from the domain, we cannot put a
concrete number) into the formula for f and try to get rid of the
sign. If we can make this extra sign disappear, that is, if we obtain
f (x) out of f (−x),
then the function f is
even. On the other hand, if we are able to pull this sign out so that we get
-f (x) out of f (−x),
then the function f is
odd. If none of this is possible, then the function is not symmetric. For
making the sign disappear or jump out we use our knowledge of
elementary functions.
Note that although usually it is easy to see whether the function is
symmetric or not, sometimes it is not so simple. In particular, sometimes it
happens that you substitute -x and get an expression that does not
look like f (x) or -f (x),
but in fact it is equal
to one of them. Such problems are quite treacherous. If in doubt, simply
write down the equation
f (−x) = f (x), put in the
concrete expression for f and try to see whether this is true for all
x or not. If yes, the function is even, if not (if it fails for even
one x from the domain), then you can be sure that it is not even.
Similarly you try to solve
f (−x) = −f (x),
and if it is not true for all x, then the function is surely not odd.
Example: Determine the symmetry of
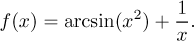
Solution:
As we saw above, the domain is a symmetric set, so the function might be
symmetric. We substitute -x:
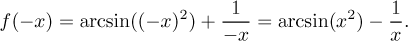
We used the fact that x2 is an even function, that is, it
makes the extra sign disappear:
(−x)2 = x2.
We got an expression and it seems that it is not equal to
f (x)
nor to -f (x). To be sure we check:
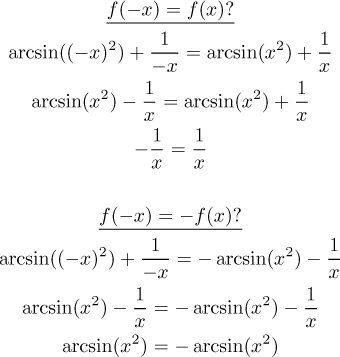
In both cases we obtained an equation that is not true for all x from
the domain. We conclude that the function is not symmetric.
Note that in the arcsin part, the sign disappeared. This shows that the
function arcsin(x2) is even. On the other hand, we were
able to pull the minus out of 1/x. Thus the function
1/x is odd.
For further examples we refer to
Solved Problems.
Periodicity
Back to Methods Survey - Basic
properties of real functions
![]()
![]()