Definition of a limit

Here we will introduce one of the most important notions related to functions: the limit of a function. Before giving a formal definition, we will try to get some feeling for what is a limit. Essentially it is the attempt to answer the following question: Given a function f and a certain point a, what happens to the values of f if we start substituting into it numbers close to a? Another possible question is this: If we stay close to a, can we approximate the values of f by some number with good enough precision?

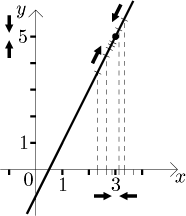
Consider the function f (x) = 2x − 1 and the point a = 3. When we substitute values of x that are close to a = 3, the outcomes are close to 5. The closer x is to 3, the closer f (x) is to 5. To put it another way, if we put a slider on the x axis, start sliding it to a (from both sides) and look at what the corresponding values of f do, we see that they go to 5.

This behavior is described by words "f converges to 5 as x tends to 3", or that "5 is the limit of f as x tends to 3".

Some things need to be emphasized to dispel two frequent misunderstandings about the notion of limit. First, the point a is not considered when looking at values in the process of limit finding; it is only the destination for x's, they get arbitrarily close to a but they are never equal to it. In fact, one can even make a limit at a although the function does not exist there. In the following picture we removed a from the domain of f, but for the limit nothing changes.

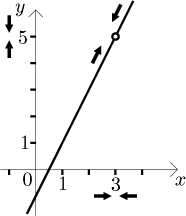
If we want to make a limit of some f at a certain point a, only one requirement is needed: There must be some x in the domain of f that get arbitrarily close to a, so that it is meaningful to say the sentence "as x tends to a". If some function g is defined on the set (0,1) ∪ (1,2), then it makes no sense to ask about its limit at 3 as the function does not exist near 3. However, we can ask about the limit at 1, since it is possible to get as close to 1 as one wishes from both sides using numbers from that set.

There is a mathematical notion that precisely describes what we just wrote, we would say that a must be an accumulation point of the domain of f. However, many authors feel that this is too technical and prefer to require a bit more. Namely, for the limit question at a to even make sense, they require that f be defined on some reduced neighborhood of a (in the previous paragraph we considered a function g defined on a reduced neighborhood of 1). This requirement is more restrictive but also more convenient; moreover, for most purposes it works; therefore we will adopt this approach here in Math Tutor. The particular choice is a matter of taste, if you look at some textbook and they start talking about accumulation points, you will know that the difference is not crucial.

The second important thing is to point out that the pictures above were too neat to give the proper idea of the limit, since the function was "nice" and also it approached its limit in a very nice manner. Nothing like this is necessary. The traditional idea "limit means that when we go to a, the function goes to L" is actually wrong precisely because it suggests that the values should go to the limit sort of directly, without any detours.

In fact, the function need not be continuous (or monotone) and while function values approach the limit, they may do it in any crazy manner they feel like, the only condition is that the values of f eventually get as close as required to the limit value. We offer here this example to show that limit may be approached in a less "nice" way than above, even uglier examples may be found in sections "saw-like" functions, sin(1/x), and Dirichlet function in Theory - Elementary functions.

What do we mean by this "eventually...as close as required"? The basic idea is that we are willing to tolerate certain distance (traditionally denoted by epsilon ε) by which f may differ from the limit value, note that in a graph this means that the values of f must stay in a horizontal strip of width 2ε around the limit value.

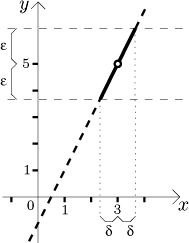
We obviously cannot hope that all the graph will be within this distance; as we are getting closer and closer to a (from both sides), the values of the function may occasionally (or often) jump out of the tolerance. However, for the limit to be true, this jumping out of tolerance must sooner or later stop. In other words, there must be some area around a on which the values of f already stay within the ε-strip around the limit value. This area around a is traditionally given by specifying how far one can go from a without running out of the strip with the graph, we use delta δ. The picture above should explain it best, another epsilon-delta situation is at the end of that less nice example.

Think of it as a game. Somebody gives you an epsilon, the tolerance, typically very small. Your task is to force the function to stay within the corresponding horizontal ε-strip around the (alleged) limit value, and the only tool you have for it is cutting away some pieces of the graph that you do not like. However, you cannot cut all the way to a, you must leave some piece of graph on both sides of a, and the horizontal size of the graph that you leave on both sides of a is the delta you have to find. If you find such δ, you won this game. Note that the value at a itself is not considered.

Of course, this would not be enough for the limit to work. The key is that for the function to have the desired limit, we must be able to win all games, no matter how small epsilon we are given by our opponent. Convince yourself by looking at the first example and the less nice one that in both cases it should be possible to win any game, even for a very very tiny epsilon. In short, for a limit to be true, the function must get close to the limit value and sooner or later also stay close as the argument approaches a.

Note that we are answering one of the questions from the beginning. Namely, if we are close to a, then the values of f can be approximated by a certain number, namely the limit, and the game actually allows us to be precise when needed: Given the tolerance, we know how close we should stay to a for the approximation to be good enough. We are ready for the definition.

Colloquial names: "f tends/goes to L as x tends/goes to a", "f tends/goes to L at a", "f has limit L at a". More details on notation can be found in this note.

The definition specifies the word "limit" as the outcome of a limit question (the number L) if it exists. However, people also use this word to denote the limit question itself, especially if it is expressed using the notation "lim( f )". So for instance one can ask "what type is the limit lim_x→a( f )" even though it may not be obvious whether this question has any meaningful answer (that is, whether there is an appropriate L as in the definition). If there is such L, then by the definition this number is called a limit. It might sound funny that "limit" (a number) is an outcome of "limit" (a problem), but this sloppiness seldom causes any trouble. Now that we understand this, we return to the definition:

If the function has such a limit (number as in the definition) at the specified point, then the limit   lim_x→a( f )   (the problem) is called convergent, or we say that this limit converges. Otherwise it (the limit problem) is called divergent, or we say that it diverges.

Note that the inequality "0 < |x − a|" removes the point a itself from consideration, we do not check whether the corresponding point is in the strip, exactly as we said before. How is such a definition used? Click here to see a correct and complete proof by definition that the very first example above was correct.

We had two examples of a limit that works. It is useful to look at what can go wrong. Consider these three situations

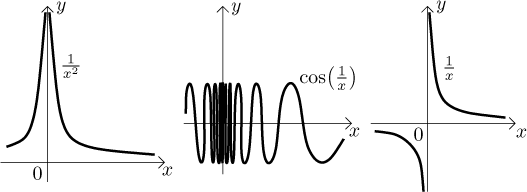
What can be said about limit at 0? In the first graph (on the left) we cannot have a limit, since no matter what number L we try, the function always runs away from it right next to a = 0, so there is no hope of getting rid of that blow up by cutting away pieces of the function some distance away from a.

In the second graph we have a function that does not blow up (at least not around a), but it keeps oscillating between 1 and −1. No matter how close we stay to a, there will always be another large oscillation there. This may need a bit more detail: The numbers 1/(kπ) go to 0. This means that every time we choose some δ > 0, one of these numbers will be in the interval (0,δ), so also the next one, 1/([k + 1]π) will be there. But the function cos(1/x) is equal to 1 in one of them and −1 in another one (which is which depends on the parity of k), which proves that no matter what δ > 0 we try, there will always be some oscillation between −1 and 1 within the distance δ from a = 0.

Consequently, there is no L that would serve as a limit. Indeed, try to choose some likely L. When somebody gives us a small epsilon, namely less than 1, then the corresponding horizontal strip around L will be less than 2 in height, so the oscillations of size 2 will jump out of it no matter where the strip actually is, that is, no matter what L you chose. And since - as we saw in the previous paragraph - these oscillations are arbitrarily close to a, there is no delta that would force the function to stay within the strip. Note that it was crucial that the size of the oscillation stays large. In the section sin(1/x) in Theory - Elementary functions there are some variations of this example, one of them also keeps oscillating but the size of oscillation decreases to zero and the limit works.

The third graph is in a sense a combination of blowing up and going in two different directions, here as we approach a from left and right simultaneously, some values jump up (on the right) and some down (on the left).

Although there are many completely crazy functions, the first two graphs are in fact typical of what can go wrong. Whenever we have a divergent limit, either there is some blowing up happening, or some oscillation that does not calm down, or a combination of both.

Recall that we had two questions at the beginning. One was: Can we approximate the given function by some number when close to a? The examples of convergence and divergence we just saw suggest that the notion of convergence exactly answers this question. Indeed, in those three divergent examples we cannot say that close to a = 0 the functions would have values close to a certain number.

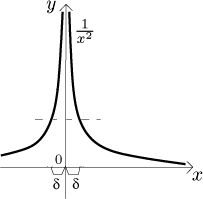
A symmetric situation gives negative infinity as limit.

Definition.
Consider a function f defined on some reduced neighborhood of a point a. We say that ∞ is a limit of f as x tends to a, or that the function goes to infinity as x tends to a, if for every real number K there is some δ > 0 so that for all x∈D( f ) satisfying 0 < |x − a| < δ we have f (x) > K.

We say that −∞ is a limit of f as x tends to a, or that the function goes to negative infinity as x tends to a, if for every real number k there is some δ > 0 so that for all x∈D( f ) satisfying 0 < |x − a| < δ we have f (x) < k.
The notation for limit equal to infinity is

The notation for limit equal to negative infinity is

We can also write "f →∞ as x→a" in the former and "f → −∞ as x→a" in the latter case.

As you can see, it is a game again, this time the opponent is choosing (for limit infinity) very large K's to make our task harder; if negative infinity was the question, the opponent would typically choose for k large negative numbers to push the function down.

We need to put some system into it, since we now have two kinds of a limit. If we have a limit by the first definition, a real number, it is called a proper limit and we have convergence. Otherwise there is divergence. There are two kinds of divergence. The nicer one is that we still have a limit, either infinity or negative infinity. These are called improper limits. If we do have a limit, proper or improper, we say that the limit exists. The "bad" kind of divergence is that not even an improper limit exists, which happens when there is some oscillation involved. We then simply say that the limit does not exist and write

To sum up, convergence is about approximating functions by numbers. If it is possible, we have a proper limit and convergence, otherwise we have divergence. Existence of a limit is the question "what happens to f when we get close to a". Either there is some answer (function goes to a certain number, it goes to infinity, it goes to negative infinity), then a limit exists, or we can't say anything definite and the limit does not exist.

Important remark: When we wrote the definition of the proper limit, we wanted the function to stay within ε of L, that is, we wanted f to stay within the ε-neighborhood of L, denoted U_ε(L). Now we wanted f to stay in intervals (K,∞) in the first case and (−∞,k) in the second. Remarkably, these are exactly typical neighborhoods of ∞ and −∞, respectively. In the first definition our task was harder when the neighborhoods were small, that is, when epsilon was small. Now to make neighborhood of infinity small, we want K to become large. Recall the definition of an ε-neighborhood of infinity: U_ε(∞) = (1/ε,∞). Note that if we send epsilon to zero (from the right, from positive numbers), then 1/ε will grow beyond any bound, that is, we are making these neighborhoods "small". Similar observation works for negative infinity. This shows that also for improper limits we can use epsilon-neighborhoods and the nature of the game does not change.

Note that the two definitions - for proper and improper limits - differed in only one place: The specification of what we want from our function f. Now it turns out that these two different specifications can be written in one common way using U_ε(L), where L could also be infinity or negative infinity. Therefore we can rewrite these two seemingly different definitions into one that would use neighborhoods, since we can also change the delta-condition to the language of reduced neighborhoods.

However, before we do it, we will introduce two more kinds of limit that will be eventually also written using this general form.

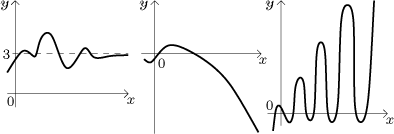
In the situation of the first graph we could say that when x is really large, the function values are about 3. This we call limit at infinity, and it is a proper limit and convergence. The two other cases are divergence. In the second graph we cannot approximate the function by some number, but we do have something to say. We have an improper limit here, namely negative infinity. The third case is the "bad one" when no limit exists, it is a typical combination of blowing up and oscillation. Note that we do not have limit infinity there, because although the function keeps going higher and higher beyond any bound, it does not stay there eventually, which does not fit with the idea of limit.

To write the definition of limit at infinity properly, we need to decide on the game. We know now how to specify the requirement, for proper limit we would want that (after cutting away unwanted parts of the function) the values of f stay within a strip given by some epsilon, for limit infinity/negative infinity we would want the function (again, just the right piece of it) to stay above/below some given bound. Now we also know that both requirements can be expressed in a common way using epsilon-neighborhoods. How do we do the cutting away business? We want to say that "given neighborhood of the limit (proper or improper, we can now handle both), the function stays within this neighborhood eventually, that is, if we stay close enough to its right end". But staying at the right end again translates to a neighborhood of infinity, this time infinity on the x-axis.

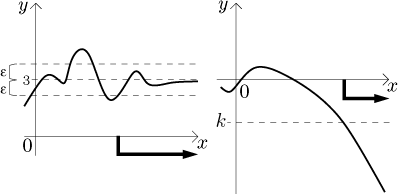
Of course, we may also look for a limit at negative infinity, provided that the function goes there. As with the limit at a, in order to be able to consider limit at infinity/negative infinity, we need the function to be defined on some reduced neighborhood of it.

Now we are ready for a general definition.

We now have four possibilities for limit. We may be looking for a limit at a proper point (at some real a) and if we find a limit, it can be proper or improper. We can also look for a limit at an improper point (at infinity or at negative infinity) and again, if we find it, it can be a proper limit or an improper limit.

Here you can look at the proof by definition that 2x − 1 goes to infinity at infinity.

To make sure that you have the right feeling for the limit, look at the following two graphs and try to guess their limits at negative infinity, −2, 0, 2, and infinity, then check that you got the same answer as us.

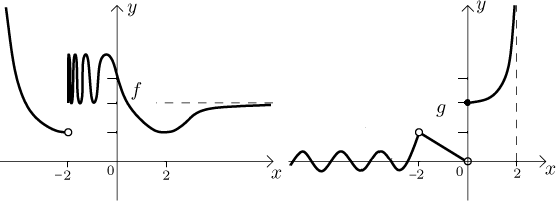
Answers:

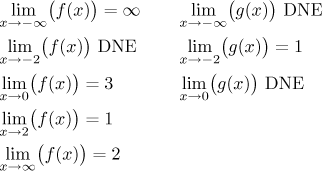
The limit of g at 2 and at infinity was not answered because the question does not make sense, the function is not defined on any reduced neighborhood of 2 and it is also not defined on any neighborhood of infinity. Note that when we say "limit DNE", it means that the question makes sense (function is defined on some reduced neighborhood of that particular a), just we don't have a nice answer. The situation with g around 2 is different, the question itself is meaningless. Note also that we have a limit of g at −2 although the function is not defined there; this should not surprise us any more, we know that the value of g at −2 has no effect on the limit at −2 and need not even exist.

The assumption about f existing on some reduced neighborhood of a may sometimes be tricky. For instance, consider the tangent around infinity. At the first glance it seems that tangent extends there, so we could look at a limit at infinity; however, the points where tangent does not exits go to infinity, so no matter what neighborhood of infinity (on the x-axis) we try, there will always be some points where tangent does not exist. Therefore we can't ask about a limit there.

When we talked about the limit at a above, we emphasized that we approached a from both sides. However, sometimes it is helpful to approach a just from one side. For instance, in the last picture above, the function f did not have any limit at −2, but when we approach a = −2 only from the left, there definitely is some tendency. We can approach −2 only from the right, too, but here we have an unpleasant oscillation and no limit. Thus we naturally arrive at the notion of one-sided limit, limit at a from the left and limit at a from the right.

Note several things. First, to have a one-sided limit, we do not really need the function on the other side of a. Therefore we can use one-sided limits in situations when we have functions only on some one-sided reduced neighborhood of a. For instance, for the function g in the picture above we can ask about the limit at 2 from the left (it does exist on some reduced left neighborhood of 2), although we could not ask about limit at 2.

Second, since one-sided limits look at a smaller part of the function, we have a better chance of getting some reasonable answer. Thus we often use one-sided limits in situations when we in fact ask about the ordinary (both-sided) limit, but the situation is difficult to handle and looking at just one side may help.

Third, we now have three kinds of limits. The original notion, then the limit from the left and limit from the right. When we say a limit, we always mean the original notion, the both-sided one we covered above. Occasionally, when we mix more kinds of limits, we may emphasize the original notion by saying "both-sided limit".

Last but not least, note that one-sided limit makes only sense for a proper a. Indeed, the limit at infinity is actually limit from the left, and limit at negative infinity is also a limit from the right. Therefore we do not talk about one-sided limits at improper points.

Now we will make proper definitions.

Definition (one-sided limit).
Let f be a function, let a be a real number such that f exists on (a,a + b) for some b > 0. Let L be a real number, ∞, or −∞. We say that L is a limit of f as x tends to a from the right if for every ε > 0 there is some δ > 0, δ < b so that for all x∈(a,a + δ) we have f (x)∈U_ε(L).

Let f be a function, let a be a real number such that f exists on (a − b,a) for some b > 0. Let L be a real number, ∞, or −∞. We say that L is a limit of f as x tends to a from the left if for every ε > 0 there is some δ > 0, δ < b so that for all x∈(a − δ,a) we have f (x)∈U_ε(L).

Note: The condition δ < b in the game makes sure that (a,a + δ) is a subset of (a,a + b), respectively that (a − δ,a) is a subset of (a − b,a), so the function f exists on these right and left reduced delta-neighborhoods.

Notation for the limit from the right:

We can also write "f →L as x→a⁺", for short we can even write "f (a⁺) = L".

Notation for the limit from the left:

We can also write "f →L as x→a^-", for short we can even write "f (a^-) = L".

We return to the two graphs above. Try to guess all possible one-sided limits and compare with the correct answers.

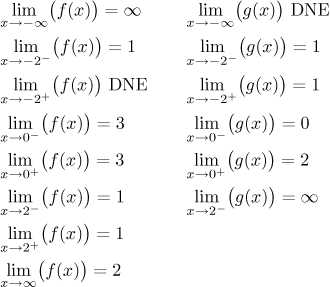
Now for g we have a limit at 2 from the left, but still no limit from the right there.

One-sided limits have properties very similar to the limit. Most theorems that are true for limits are also true for one-sided limits, as we will see in the following sections. Here we will put a theorem that ties up the two notions. Note that since the definition of a one-sided limit requires less than the definition of a limit, it follows that if L is a limit of f at a, then it is also automatically a limit at a from the left and a limit at a from the right. The other direction requires existence and equality.

Theorem.
Let f be a function defined on some reduced neighborhood of a real number a. Let L be a real number, ∞, or −∞. Then L is a limit of f at a if and only if L is also a limit of f at a from the right and from the left.

We can express the condition using the short notation like this: lim_x→a( f ) = L if and only if f (a⁺) = f (a^-) = L.

Important remark: Note that the notion of a limit is a local notion. This means that the outcome depends only on what happens immediately next to the limit point, the behavior of f further from a is totally irrelevant. (For completeness we recall that also the value of f at a is irrelevant.) We can say it like this:

Let f and g be two functions, consider a point a. If there exists a reduced neighborhood of a, however small, on which f = g, then the limits of f and g at a are equal.

This is sometimes quite useful, we can carefully replace an unpleasant function by a better one as long as they are the same on some reduced neighborhood. Of course, analogous statements work for one-sided limits and one-sided neighborhoods.

We conclude this section with a theorem that is not exactly very useful but it shows that the notion of the limit is reasonable:

Theorem.
If a functions has a limit (both-sided, one-sided) at some a, then this limit is unique.

In other words, it is not possible to have two different limits in one situation. From now on we are justified in talking about the limit instead of a limit.

Basic properties, evaluating limits
Back to Theory - Limits