
Here we will try to guess the limit of a function at infinity, of course we will also show how to confirm such a guess. We will look at functions that involve all kinds of powers (polynomials, exponentials) and logarithms, we will show more precise specifications below.
Note that some of these considerations would also work for limit at negative infinity, but it may be tricky and treacherous. There's a little trick which does it safely for us: Given a limit at negative infinity, use substitution to change it into a limit at infinity and all the tricks from this section apply.
The guessing we will cover here is very useful and usually offers the shortest solution to expressions that would otherwise have to be solved in different ways, often using l'Hospital rule leading to complicated expressions. It uses two basic ingredients. The first is a good knowledge of the limit algebra, especially the basic limits, the second important ingredient is the understanding of interplay of powers and exponentials (and roots). We will start with little introduction.
In many functions one finds sums of powers and similar expressions. For
instance, consider the function
Now here's a problem: What is the limit at infinity of
By the way, when we are adding and subtracting some objects and even multiplying them by real numbers like we did in the above example, we call it "linear combination". So the expression in this example was a "linear combination of powers". We will use this terminology throughout this section. First we will identify what kind of problems we will address.
Note that negative powers do not cause troubles in expressions like the one
above, we saw that x−2 tends to zero at infinity and
therefore does not cause troubles in the limit algebra when added to
something else. Therefore we will only consider positive exponents in this
section. If the exponents also happen to be all integers, we are actually
talking polynomials here. But we will work in more generality and also allow
for positive exponents that are not integers (for instance the exponent
We will also allow for "exponentials", that is, powers of the form
But that is not all. While "linear combinations" of powers and exponentials
as above (powers/exponentials multiplied by numbers and then
added/subtracted) appear quite often, we will include still more expressions:
logarithms and even powers of the form
Question:
We have an expression of the formα⋅A(x) + β⋅B(x) +..., where the functionsA(x), B(x),... can be powersxa witha > 0, exponentialsax witha > 1, powers of logarithms[ln(x)]a witha > 0, and general powers likexx. What happens with this expression if we let x go to infinity?
Note that all expressions listed above tend to infinity as
Solution to the problem:
If we letx→∞, then an expression as above will behave exactly like its dominant term. To prove it mathematically, we factor the dominant term out of the expression and then apply the limit. The expression that remains after factoring should tend to a non-zero real number.
By a "dominant term" we mean the term that, for large x, prevails over
all other terms in the given linear combination, and so the other terms can
be ignored, they do not interfere with the tendency that the dominant power
has around infinity. There is a hierarchy among all the types listed above
(powers, exponentials, logarithms,...). When we say that "term A
prevails over term B for large values of x", we really mean
that when investigating limit of the expression
Example:
We will shortly see that
Of course, this result is just guessing. We wrote above (in Solution) that mathematically we can do this by factoring out the dominant term. We try it:

Note that the term that remained after factoring out the dominant power
indeed tended to a non-zero real number, exactly as stated above. The fact
that it is non-zero becomes important for limit algebra, we can't get
There is a way to write our intuitive reasoning properly. When we write
Note that this handy way of writing is not universally accepted. Also, it does not constitute a proper solution - after all, we were just guessing there. Any answer that we get in this way should be confirmed by a correct mathematical calculation, for instance the factoring out procedure that we have shown above.
When we look at powers in a linear combination of powers and other similar
terms, we actually do two different things. First, we look just at the
powers, exponentials etc., that is, we ignore the multiplicative constants
before them. In this way we determine the type of an expression. For
instance, the expression
This type is used when roughly comparing behavior of different
expressions, finding out which can be ignored etc. Then when we really start
guessing the limit at infinity, we do have to include the multiplicative
constants in our reasoning. Thus we would say that
As you can see, the intuitive procedure can be simple, writing it properly mathematically (by factoring) may be a bit longer but should never be tricky, as long as we correctly identify and factor out the dominant term. Which brings us to the main part of this section:
Here is the list of the terms mentioned above from the most dominant to the least. That is, every listed expression prevails over all expressions listed later:
(1) the power xx,
(2) the exponential ax for
(3) the power xa for
(4) the logarithm [ln(x)]a for
For practical use people often prefer a more colloquial way of remembering this hierarchy, using phrases like "powers beat logarithms at infinity" and "exponentials beat powers at infinity" etc. Proofs of this hierarchy are shown for sequences in this note, for functions it can be proved in essentially the same way.
When investigating a linear combination of such terms, we always first find the dominant expression. However, there may be more terms of this dominant category. Thus we also need to know mutual dominance within each category. There the rule is simple. In categories (2), (3) and (4) there is always a parameter (i.e. a) and the highest one is the dominant one.
In fact, the question of dominance is one kind of an answer to the question "which infinity is larger". In the following picture (not quite to scale) we will try to express symbolically the relationship between different kinds of expressions, obtaining the scale of powers:
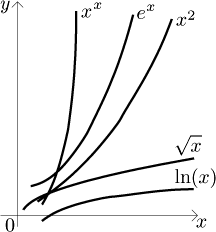
Example:
What is the limit of
Solution:
There are three categories there: exponentials, powers and logarithms.
Exponentials are the highest on the list, so they will supply the dominant
term. There are two candidates, 2x and
3x. Since
How do we confirm this result mathematically? By factoring the dominant term out.
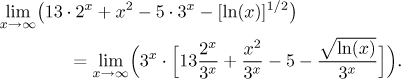
The three fractions in the parentheses are best handled separately. The first one is just an exponential, the other two will lead to l'Hospital's rule:
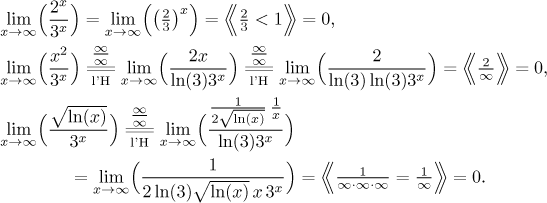
Finally we get
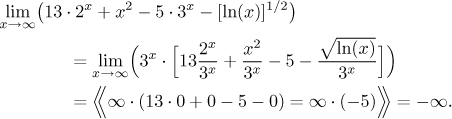
Note that sometimes we can apply this reasoning even for terms that do not
look exactly like those above, but can be changed into them by algebra.
Two most typical examples:
The intuitive procedure also works if there are some roots mixed in the expression; that is, if some parts of the expression are closed under roots. We then follow the following procedure. First we handle each root individually. For every root, we find the dominant term of the expression inside this root, this determines the type of the expression under the root. When we apply the root to this expression, we obtain the type of the root as a whole. We can confirm this by factoring it out, the resulting root then should have a proper non-zero limit at infinity.
After handling the roots (if any), we put all the types together (those that were by themselves, and types of roots) and determine the dominant term of the whole expression. This procedure may be repeated several times, in case there is a root under which there is an expression with another root and so on. Finally, having determined the dominant term of the whole given expression, we can handle it as above; that is, we factor out the dominant expression and check the limit.
Note: The factoring out part is usually easier when one repeats the guessing part; that is, first factor dominant terms from the roots and then work your way out.
Example: Find (if it exists)
![]()
First we check on the root. There are just powers under it, so they are in
the same category and the one with higher exponent wins. In our case, the
expression under the root is of the type x6. When the root
is applied to this, we find that the root itself is of the type
![]()
We obtained our guess (on the way we saw that the root by itself behaves like
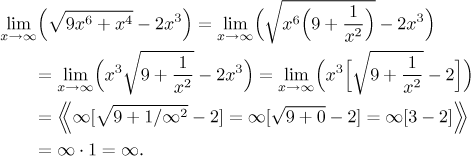
In fact, the guessing part above might have been wrong and we would not know it, because we did not cover an important topic yet. We got lucky there, but now it is a time for
Warning: What happens if we get several dominant terms? If they are
added, we can add them safely. If they are subtracted (that is, if the limit
algebra would lead to the indeterminate form
For example, if we had 4x6 instead of
Why is it so? Because when we guess, each term actually represents not just
itself, but there may be other terms of lower importance hidden in it (like
Compare the following two examples; they might look silly, but they illustrate the point well. In each of them we do the guessing first (even if it might be wrong) and then do the proper calculation.
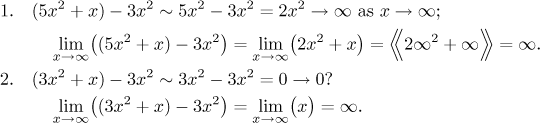
In the first example, the guessing is correct; note that in the proper
calculation, after putting the terms together, we can still ignore the
Rule for dominant terms: If we are evaluating a limit at infinity by guessing and there are more dominant terms in an expression, then we can put them together by algebra only if they do not cancel as a result.
If they do cancel, we have to give up on intuitive calculations and try some other method. However, even then this guessing part helps as a preparation, since it is often useful to know the types of terms in an expression.
Remark: We talked about roots, but these are just special powers
(the square root is just the
We now reached the most typical expression that can be handled using the intuitive calculations: a fraction whose numerator and denominator are of the type we described above. How do we handle such fractions? First we separately investigate the numerator and denominator: We determine the dominant term of each of them, then factor them out. Then we have one dominant term in the numerator, one in the denominator, so we cancel them if we can and finally we find the limit of the resulting ratio. The scale of powers can again help here. If the term in the numerator prevails, we get infinity as the limit at infinity. If the term in the denominator prevails, we get zero as the limit at infinity.
This is quite natural. We usually get an infinity over infinity situation, and prevailing means that one infinity is larger than the other infinity, so it wins. For instance, when the infinity in the denominator prevails over the infinity in the numerator, it means that the denominator is eventually much much bigger than the numerator and the resulting ratio is thus very tiny, which suggests that it goes to zero.
We mentioned that sometimes the dominant terms of the denominator and numerator can be cancelled when they are factored from the ratio; we then obtain the type of the fraction as a whole.
Sometimes when facing a ratio, people prefer cancelling to factoring out and comparing. It works - but only sometimes. We offer a thorough discussion of how to handle ratios of polynomials at infinity in this note.
Example: Find (if it exists)
![]()
First we will guess the answer intuitively, then do it by proper calculations. We should start by handling the roots.
In the cubic root, the dominant term is the cube, therefore we can ignore the other terms for large values of x. In the square root in the denominator, the exponential prevails over the square and so we can ignore the power.
![]()
Now we know the types of the roots at infinity, so we can compare them with the remaining terms and find the dominants, separately for the numerator and denominator. Then we use the hierarchy of powers to guess the outcome:
![]()
What was the reasoning? In the numerator, powers beat logarithms, and the highest power is the square. By the way, this shows why it is important to always handle roots first. At the first glance one would guess that the x3 is the dominant term in the numerator, but after we analyzed the root, we saw that it actually behaves just like x.
In the denominator, the dominant term was the exponential 2x, so we ignored the rest. Finally, since exponentials beat powers at infinity, we concluded that the ratio converges to zero.
Now we are supposed to confirm our guess by calculations - namely factoring out. Although an experienced student would do it on a few lines, we prefer to show more detail and also add a remark concerning the two roots; therefore we offer the calculations here.
Although it does not happen often, sometimes expressions of the above type are multiplied together. In such a case one applies the intuitive procedure to each term of the product, finding the type of each. The type of the whole product is then the product of individual types. However, usually one does not get one of the types studied above (powers, exponentials etc.), rather a product of such types. Such expressions are not listed in our scale of powers, therefore it is rare to get a ready answer this way. However, often one can use experience with types to find out something useful anyway.
Example:
![]()
Note that we found out that the numerator is of the type
![]()
Now we are comparing (after cancelling) two types,
The answer is: no. In fact,
The intuitive reasoning can be applied to even more complicated expressions. It would be difficult to express precisely where we can apply this kind of reasoning, but less precisely it goes like this: The basic building block is a linear combination of powers, exponentials, powers of logarithms, and general powers (their multiples added and/or subtracted). This basic combination can be put under some root/into a power, thus creating a new building block that can be a part of another linear combination. These linear combinations can be put together using ratios/product and so create new members of further linear combinations. All these procedures can be repeated in any order.
Warning: Above we freely ignored parts of linear combinations and
later even roots when they became unimportant compared to some dominant
terms. However, there are two things one should be careful about. First, we
can ignore only in linear combinations; roots/powers and ratios/products can
be ignored only when they get replaced by their dominant terms and thus
become eligible parts of linear combinations. Second and more importantly,
this ignoring business can be only done in expressions as outlined above
(linear combinations, roots/powers and ratios/products mixed up). It is not
permissible to do ignoring in expressions which are mixed up with other
functions. For instance, we can replace x − ln(x)
with just x if it is under a root or a part of a fraction, but we
cannot do it if it is an argument of, say, exponential. Thus
For many examples we refer to Solved Problems - Limits.