Problem: Find the derivative of

Solution: The function is given by an expression, so we can use rules to find its derivative. Since this function has x both in the base and in the exponent, it is a general power. Thus we have to change it into its canonical form before doing anything with it.

This function has the form of a composed function, the outer function (that is, the operation that is done last when evaluating) is the exponential e^y (whose derivative is e^y). We apply the chain rule, as usual differentiating first the thing that is done last when evaluating.

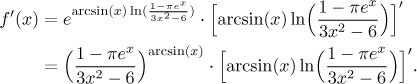
Since the first term (the general power) will be copied in all subsequent steps, we will replace it temporarily with a diamond shape. The expression we need to differentiate now is a product of two terms (that is, the last operation performed is multiplication), hence the product rule is to be used.

The derivative on the left is elementary, on the right we need to differentiate a composed function using the chain rule, on the outside (done last when evaluating) we have ln(y) with derivative 1/y, so we start with it.

Now we need to apply the quotient rule.

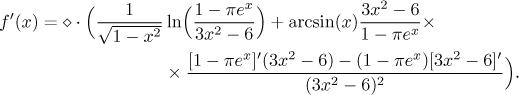
Both expressions to be differentiated are linear combinations of simple terms, so we finish the calculation.

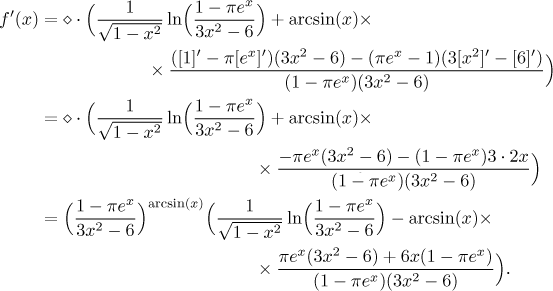
Now we need to find the domain. We start with the given function. As a general power it has to be investigated in its canonical "e to ln" form. The arcsine rules out any x with |x| > 1, so we can right away restrict our attention to [−1,1]. The next condition is that the fraction in the logarithm must be positive. For x from the range [−1,1], the denominator is negative, so we need the numerator to be negative as well, which is true for

x > ln(1/π) = −ln(π).

However, note that ln(π) > 1, so in fact this condition is true for any x from [−1,1]. Thus

D( f ) = [−1,1].

Since we can only do derivatives on open sets, we lose the endpoints, but for other x from the domain of f the derivative exists. We get

D( f ′ ) = (−1,1).

Next problem
Back to Solved Problems - Derivative