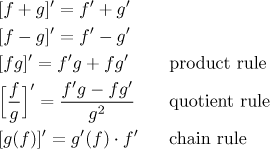
If you wish to simultaneously follow another text on derivatives in a separate window, click here for Theory and here for Solved Problems.
Here we will show the algorithm for calculating derivatives. Differentiation is the basis for most calculations in real analysis, so you should master it well. The desired level of mastery is simple: You must be convinced that you can find (without too much thinking) the derivative of any function that comes your way, assuming it is put together using elementary functions and algebraic operations/compositions. The algorithm outlined below is capable of exactly this.
In order to be able to differentiate, one needs to know by heart two basic
things:
Dictionary, that is, the
elementary derivatives.
Grammar, which means the basic five rules for operations:
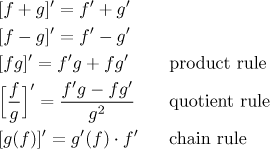
It is also handy to remember that derivative is linear, that is, when differentiating sums, we differentiate each summand separately; moreover, multiplicative constants can be pulled out of derivative.
There are two possibilities for derivatives. Sometimes we can use elementary
derivatives and write the result right away. However, note that we can use
the formulas for elementary derivatives only exactly as stated, any
modification means that formulas no longer work and we have to use rules.
For instance, while we can write that derivative of
The second possibility is that we have an expression that is not on the list of elementary derivatives. Then we have to use rules to break it down to its building blocks, which are finally done using elementary derivatives. The algorithm for this is below, but before we get to it, one remark concerning notation.
Beginners have sometimes problems with the application of the derivative
symbol, for instance they may get confused by the notation for the chain
rule above. In fact it is simple. We start with an example. Consider the
function
Algorithm for derivative.
Step 1. Look at the expression that is supposed to be differentiated
and identify the operation that is done last. It can be an algebraic
operation or an outer function in a composition. If you need a refresher on
this, check out the
note on order of
evaluation.
Step 2. Depending on the "last operation", apply the appropriate
grammar rule. The rule breaks the differentiated expression into simpler
expressions, some of them have to be differentiated.
Step 3. Check out the derivatives that came out of the rule from Step
2. If all of them are elementary, use your dictionary. You are done. If some
derivatives are more complicated, for each of them repeat the process
starting from Step 1.
Note that none of the above rules or elementary derivatives applies to
general powers. These have to be differentiated in their canonical
form
f g = eln( f )g.
There is also no rule for differentiating the absolute value. Functions that
feature it have to be rewritten as split functions, see below.
Warning! The results that we obtain by this procedure give derivative only at points such that the given expression exists on their neighborhoods. This means that we can use this algorithm to find derivative of a function only at points on whose neighborhoods the function is defined by one formula. What happens if this is not true, for instance if f is given by one formula on the left and a different formula on the right of the point where we want the derivative? The correct procedure is outlined below.
Derivative as an intuitive procedure. While there are more ways one can remember and apply the rules, I had best results with the intuitive "differentiate and forget" approach. Differentiation is a bit like peeling an onion. You always see only the outermost layer, the operation that is done last. Everything else, no matter how complicated, is irrelevant at the moment except that it participates as whole units in the outermost operation. You need not worry about it, since it is "hidden" by the outer layer. When you apply the appropriate rule for the outer operation, this particular operation is done for and you do not have to worry about it again (apart from having to copy things that come out of it), once it is differentiated (by applying the rules), you forget about it and pass to the next layer; since we are done with the outer layer, the next one is exposed.
This is best seen in the chain rule. For instance, when we differentiate
[cos(g(x))]′ = −sin(g(x))⋅[g(x)]′.
How does it fit with the above? The outermost operation is cosine and we do not care what is inside the cosine, the cosine hides it from us. So we differentiate the cosine, the chain rule says that we have to substitute the inside expression into the derivative of the cosine and then do "times". At this point the cosine is done with, gone from the problem, we finally see what was inside it and it is time to differentiate it.
Similarly we can interpret for instance the product rule. When we want to
differentiate f ⋅g, we at the moment do not care
what the individual factors are, we only focus on the outer operation. The
rule says that to differentiate this operation, we have to pass to the
expression
As we said earlier, this is just one of possible approaches to derivatives. Some people prefer different ways, for instance purely formal (they would at each step make notes which parts are f and which are g and apply the rules literally). Choose whichever way fits you best.
Example: Find the derivative of
![]()
Solution: The last operation performed is multiplication, the given function is a product of the bracketed term and the fraction. We therefore apply the product rule.
![]()
We obtained two terms with derivatives, none of them is an elementary function. Thus we handle each derivative as a new problem.
The bracketed (first) expression had addition as the last operation. It is not clear which of the two additions is last, but we do not care since linearity tells us that we simply differentiate each term separately.
The second differentiated term is a clear-cut fraction, we use the quotient rule.
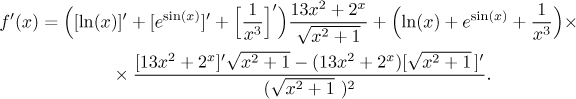
Now we have lots of derivatives, we take it from the left. Logarithm is an
elementary function whose derivative is in the dictionary. The second term is
more complicated. The last operation we do there is the exponential, so it is
a composition and we have to use the chain rule, for instance in the form
On to the last fraction. The first term on the top is a linear combination, so we use the fact that derivative is linear. In other words, we know that we should take the derivative of each summand separately, and in the first one we can pull out the multiplicative constant out of the derivative. The second differentiated term (at the end) is a composed expression, as a last we do the square root, so we apply the chain rule.

Almost there, again we take it from the left. Derivatives of sine and x−3 are in the dictionary. In the last fraction we again have elementary derivatives of x2 and 2x. The last derivative is a sum, so we differentiate each term separately.
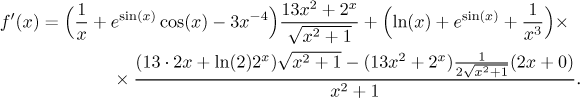
It remains to polish it up a bit and find the domain. We rewrite the negative power as a fraction as it looks better this way. Also, the big fraction simplifies quite a bit if we pull the root in the second term of the numerator out of the numerator.
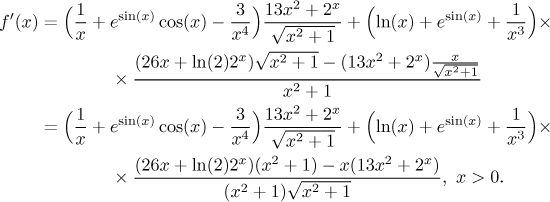
Note that the domain is just
Some notes:
1. If we do not change 1/x3 into a negative power but apply
the quotient rule to it, we get the same answer, it is just a bit more
complicated.
![]()
2. What happens if we forget that multiplicative constants can be
pulled out of the derivative? Instead of the simple calculation
![]()
3. An experienced differentiator would not write all the steps. When applying the rules to a given expression, the expression gradually "blossoms" or "grows branches", gets more complicated with every step. However, there is a logic to this and if you are experienced, you can keep quite a bit of it in your head. Thus one often writes directly the answer, building it piece by piece. When the given expression is more complicated, this can be dangerous, since it is easy to forget while differentiating one part that another should be done as well, one can also mix up bracketing. A good safety measure is to go the middle way. Do in your head only as much as you can safely keep and simplify the overall picture by leaving some parts "for later" using the []′ notation. For instance, the above example might be done in two steps like this:

Question: Find
The best case: If the function f is given by a certain expression on some neighborhood of a, we can find the (both-sided) derivative using the above algorithm and the one-sided must then be the same.
The typical case: The function f is given by a certain
expression on some right neighborhood
![]()
in other words, we find the derivative of the expression using the above
algorithm for
Other cases: Quite a few things can go wrong, it is impossible to cover all possible cases. In general, if we cannot use the above tricks, we usually go back to the definition and try to work it out.
Question: Find
Obviously, we use appropriate modifications of the above procedures.
Split functions are functions that are defined by different expressions on different sets (see Introduction in Functions - Theory - Real functions). We will ignore monsters and focus on reasonable split functions, those whose definitions are based on intervals that go one after another and there is a finite number of them (some intervals may be degenerate, that is, one point).
Procedure: Consider a "reasonable" split function f.
Step 1. For each non-degenerate interval in the definition of f
we find the derivative of the appropriate expression that gives the function
there. This result then also gives the derivative of f on the
interior of this interval.
Step 2. If the domain of f is covered by the interiors from Step 1,
we are done. Otherwise there are points in the domain of f that are not
covered by the interiors above and we need to investigate f ′ at
these points. Consider one such point a.
a) If this point is an endpoint of an interval from the definition and
also an endpoint of the domain, it means that f is defined on some
right or left neighborhood of a but not on the other side. Therefore
there is no derivative, but there might be a one-sided derivative. We
investigate it as described above. Note that if f is not continuous
from the right/left at a, then it cannot have an appropriate one-sided
derivative there, so we do not have to bother looking for it.
b) The other interesting case is that a is in the interior of the domain, but not in the interior of any of the intervals from the definition of f. Then f is most likely defined by different formulas to the right and to the left of a. Thus although there is a chance for the usual both-sided derivative, we cannot use the algorithm above (see the Warning there). Again, if the function is not continuous at a, we know right away that there is no derivative.
Assume therefore that f is continuous at a and defined by two different expressions on the right and on the left of a. Then we can find one-sided derivatives using the limit trick as described above and compare them. If the one-sided derivatives agree, they also give the derivative of f at a.
Example: We find the derivative of the absolute value
Since there is no rule for absolute value, we start by getting rid of it:
![]()
Since f is defined by the expression x on the open interval
![]()
It remains to find the derivative at 0. The absolute value is continuous there, we have nice expressions on the left and on the right, so we can use the limit trick:
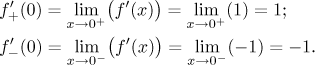
Thus the answer is
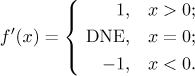
For more examples of derivatives see Solved Problems - Derivative, but obviously derivartives are used in Solved Problems on other topics in chapter Derivatives as well.