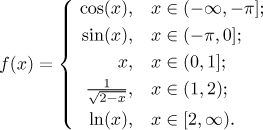
Problem: Find the derivative of

Solution: This is a function defined by cases. We start by observing that at interiors of intervals that appear in the definition we can find the derivative by differentiating (using the usual rules) the appropriate expressions from the definition.

Thus for x < −π we have f ′ = [cos(x)]′ = −sin(x), similarly we work on other intervals. In the fourth interval we use the chain rule several times after rewriting the expression into a power form:

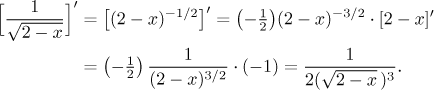
We get

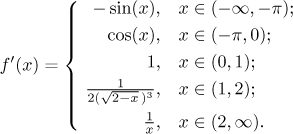
Now we need to explore situation at proper endpoints of the intervals. First we need to look at continuity. Why? If we know that a function is not continuous somewhere, then it cannot be differentiable there and we are done. On the other hand, if a function is continuous at some point, then we have one assumption satisfied in the theorem (in Theory - MVT - Derivative and limit) that allows us to find one-sided derivatives there using limits of derivatives. Fortunately, we need not look at continuity here, since we have already explored continuity of this function in Functions - Methods Survey - Basic properties - Continuity.

What do we know about x = −π? The function is not continuous there, so there is no derivative.

At x = 0 the function is continuous, so we look at one-sided derivatives there using the theorem mentioned above.

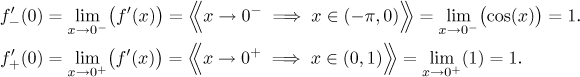
Since the one-sided derivatives agree, we have f ′(0) = 1.

At x = 1 the function is also continuous, so again we look at one-sided derivatives there using the theorem.

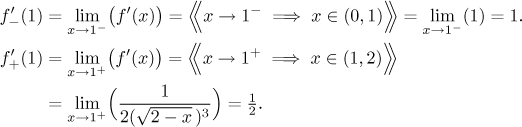
Since the one-sided derivatives do not agree, there is no derivative at 1.

At x = 2 the function is not continuous, hence also not differentiable.

We can express the answer by including the point 0 in appropriate variants.

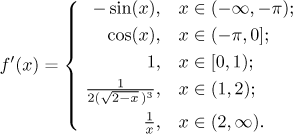
By th way, in Functions - Methods Survey - Basic properties - Continuity you will find a picture of this function, it might help you visualize things that we calculated here.

Back to Solved Problems - Derivative