Problem: Prove that for all numbers t ≥ 0 we have

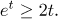
Solution: Denote f (t) = e^t and g(t) = 2t. We need to prove that f ≥ g on the interval I = [0,∞). Since algebraic reasoning seems out of question, we will try to use a theoretical approach, namely using derivative as described for instance here in Methods Survey - MVT.

First we check on how these two functions compare at the left endpoint of I: f (0) = 1 and g(0) = 0. Thus f (0) > g(0), that's a good start. Now we compare their derivatives at the interior of I. We have f ′(t) = e^t and g′(t) = 2. If f ′ were always (for positive t) at least as large as g′, then the function f would start larger at the left end of I and grow at least as fast as g, thus it would be larger on the whole I. Unfortunately, this is not true, e^t is less than 2 for small positive t. Thus the function g grows faster at the beginning of the interval I, so it is quite possible that is catches up with f and even passes it before f starts growing faster again. Thus this approach failed.

Remark: Consider the function h(t) = t. Again we have f (0) > h(0), but this time also f ′ > h′ for t > 0, since h′(t) = 1. Thus the above algorithm does work now to prove that in fact e^t > t on the interval I. Note that the exponential is always positive, so this inequality is trivially true also for negative t. Consequently, e^t > t for all real t. Similarly, we also have e^t > 2t for negative t.

This brings us back to our problem. What do we do with the unpleasant 2 in g? Note that the question above is really a question of how fast the line 2t grows, whether it manages to intersect the graph of the exponential or not. We saw that the line given by t does not, obviously the coefficient (slope) 1 is not large enough. If we start increasing this slope, then the line starts growing faster, eventually first touching the exponential and then (with still larger slope) crossing it.

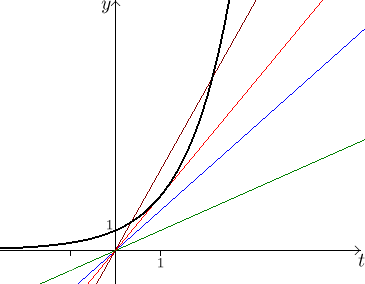
(The line given by t is marked in green. To make the picture nicer we did not use the same scale on horizontal and vertical axes.) Where does the given line 2t fit in? To see that it is better to change the setting. We actually proved above that the function e^t − t is positive on I (even everywhere), similarly it would be enough to prove that the difference d(t) = e^t − 2t is positive (or zero) everywhere, in particular on I. How can we do such a thing? Quite easily, we find the minimum of d and then check whether it is negative or not.

For that we have a standard algorithm. Note that at both ends (infinity and minus infinity) the function e^t − 2t grows to infinity, thus its global minimum (or possibly more of them) is to be found somewhere in the middle, at a critical point. From the derivative d′(t) = e^t − 2 we get one such point, t = ln(2), so the value of the global minimum is

d(ln(2)) = e^ln(2) − 2ln(2) = 2 − 2ln(2) = 2[1 − ln(2)] > 0.

This proves that d is always positive, therefore also e^t > 2t for all t.

Bonus problem: We saw that the line given by 2t does not overtake the exponential, by the way, it is marked blue in the above picture. From the picture it also seems that still faster lines could make it. Where is the dividing line? Precisely, for what value A does the line given by y = A⋅t touch the exponential?

We again use the approach via minimum. Let's make a picture corresponding to this point of view. We are actually looking at the curves below representing the differences between the exponential and various straight lines given by A⋅t, and we would like to know which of them has its minimum equal to zero.

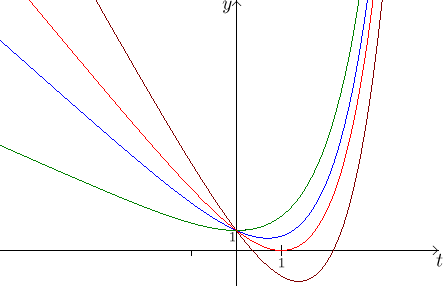
We proceed as before. First we consider the function (with parameter A) given by d(t) = e^t − At. Its derivative is d′(t) = e^t − A, solving the equation d′(t) = 0 we get the only critical point t = ln(A). It shows where the global minimum of d is attained, its value then is d(ln(A)) = e^ln(A) − A⋅ln(A) = A − A⋅ln(A) = A⋅(1 − ln(A)). We see that this minimum is equal to zero exactly if ln(A) = 1, that is, for A = e.

Conclusion: The line given by y = e⋅t touches the graph of the exponential. For 0 < A < e the lines y = A⋅t lie below the exponential, for A > e these lines cross the graph of the exponential at two points.

Next problem
Back to Solved Problems - MVT