There are three topics here: Global extrema, global extrema with constrains, and word problems on optimization.
Problem: Find global extrema of a function f over a set M.
Case 1: The function is continuous on M, which is a bounded closed set consisting of a finite number of closed intervals. Then there always is a maximum and a minimum.
Algorithm:
Step 1. Collect candidate points. These are: a) all endpoints of
intervals of M; b) all points from M where the derivative
f ′ is 0 or does not exist (or we suspect that it might not
exist).
Step 2. Substitute all candidates into f and compare resulting
values. The point that gives the largest of these values gives
Case 2: The function has a finite number of discontinuities on M, which is a union of a finite number of intervals.
Algorithm:
Step 1. Collect candidate points. These are: a) all endpoints of intervals
of M (including infinity/negative infinity if it is an endpoint); b) all
points from M where the derivative f ′ is 0 or
does not exist (or we suspect that it might not exist). Note that this also
includes all points of (suspected) discontinuity.
Step 2. Substitute all candidates where f is defined into
f; for candidates where f is not defined (open endpoints of
intervals, may include improper points) or where f may not be
continuous we also evaluate all possible one-sided limits. Compare all values
thus obtained (both by substitutions and limits).
Step 3. If the largest value is (also) obtained by substituting a
candidate, then the point that was substituted gives
If the smallest value is (also) obtained by substituting a
candidate, then the point that was substituted gives
For more details see Global extrema in Theory - Applications.
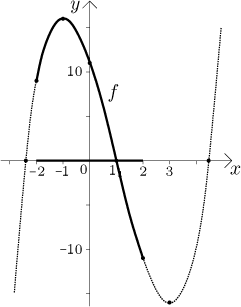
Example: Find maximum and minimum of
Solution: Since f is continuous on M, which is a bounded closed interval, there exists both maximum and minimum and we can use the first algorithm.
The derivative is
f (−2) = 9, f (−1) = 16, f (2) = −11.
We compare these values and reach the conclusion:
max[−2,2]( f ) = f (−1) = 16, min[−2,2]( f ) = f (2) = −11.
By the way, the graph of f shows what is really happening in our calculations.

Problem: We need to find global extrema of a function with more variables, but those variables are tied together by conditions whose number is one less than the number of variables.
Solution: Use the conditions to get rid of all variables but one, then you are in the above situation and the algorithm applies.
For examples of global extrema and global extrema with constraint, see Global extrema in Theory - Applications and Solved Problems - Applications.
A typical word problem on optimization describes some situation and then asks for a solution that is optimal with respect to some measurement (cost etc).
Algorithm:
Step 1. Read the problem carefully and identify all important
quantities. Use them to express the data given in the problem.
Step 2. Identify the quantity that is used to evaluate different
solutions. This quantity should be maximized/minimized. If it has only one
variable, use the algorithm above. Otherwise try to find some relationships
between variables to eventually reduce their number to one. Then use
the algorithm above.
Example: There are two access points, one on each bank of a straight
river of width
Solution: Obviously it makes no sense to consider other trajectories than straight lines across water and then over the land. What is unknown? The point on the opposite shore where we should head to. We need some variable to mark it and choose where zero is, probably the most natural choice is to put zero directly across the river.

The value to minimize is the cost C. We have one variable x and
the optimized function C that obviously depends on x, we need
to know how. The distance over the land is clearly
![]()
We want to find the minimum of this function over the interval
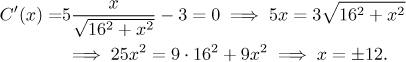
The negative solution is no good, so we have our first candidate,
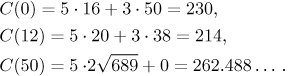
We see that the fastest way to a drink is to go across the river aiming at
the point on a bank that is
For other examples see Global extrema in Theory - Applications and Solved Problems - Applications.
Taylor polynomial and
approximation
Back to Methods Survey -
Applications