This method is based on this mathematical theorem. The formula from this theorem
![]()
tells us how to calculate. What do we see? We write the expression in the
integral that we want to evaluate in the form of a product of two
expressions and denote one of them
The new expression on the right can be evaluated with a bit of luck (if we chose f and g well). Let's see a typical example, we will also show the customary notation for integration by parts:

We remark that authors use various notation for integration by parts, some use f and g but put the derivatives in the opposite way (derivative of g on the left, f on the right), others prefer different letters (u and v seem popular) and there is even a versio with differentials:
![]()
The previous example would then go
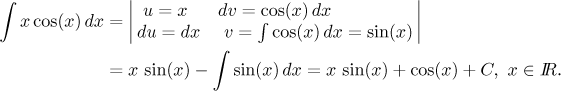
Of course the particular formula we use makes no difference, you are welcome to choose whichever you feel like. I am sort of partial to the one with differentials, but I have a feeling that the one we used first is most widespread, so we will stick to it in Math Tutor. Actually, an experienced integrator does not use any formula at all. In the given integral, we integrate one part, which gives us the middle term, and then differentiate the other part, giving them the expression for the new integral.
What are the limitations of this method? Obviously, it cannot be applied to an integral of an expression that is not a product. But even when it is, the success is by no means guaranteed. We will show the main problems on the following integral.
![]()
We try a similar choice as before.
![]()
We've got an integral for g which cannot be solved by methods covered
in Math Tutor, in fact it is a rather tough one. So this is the first
consideration: When considering candidates for f and
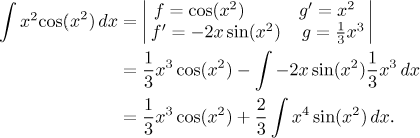
Now integration by parts did succeed, but the new integral is actually even worse then before. So it was no good, although it worked. This is the second factor to keep in mind when considering integration by parts. Actually, this integral cannot be solved using integration by parts.
Experienced integrators know that some types of integrals are just made for integration by parts. For practical tips see Integration by parts in Methods Survey - Methods of Integration.
By the way, integration by parts is sometimes also called integration "per partes", which is the same but in Latin.
This is basically the same as integrating by parts in an indefinite integral. Obviously, the new integral will also be definite with the same limits, and the middle part is actually a finished part of an antiderivative, so we use it to evaluate according to the Newton-Leibniz formula.
![]()
For a simple example we return to the first example above.

The rest is easy.
Next section: partial fractions
Back to Theory - Integration