We are given a sequence of functions
Question 1: Investigate (pointwise) convergence of the given
sequence of functions.
Solution: Consider a general x from the intersection of domains,
take it as a fixed parameter and evaluate the limit of the sequence of real
numbers
For some x this will diverge. For some x this limit converges,
call the resulting number
Question 2: Investigate uniform convergence of the given
sequence of functions.
Solution: First, find the limit f of
Next, guess a set M (a subset of the region of convergence) on which
you suspect uniform convergence. Typically you start with the region of
convergence, or the region of convergence without small neighborhoods of its
endpoints.
For a fixed k, evaluate
Mk = sup{| f (x) − fk(x)|, x from M }.
If
If not, then most likely the set M is too ambitious. Try to guess a
smaller set, analysis of the suprema above may help in identifying which
parts of the original M caused troubles.
Example: Investigate convergence of the sequence
![]()
Solution: First we investigate convergence. We consider x to be a parameter and evaluate limit in k.
![]()
This limit existed for all values of x, so the region of convergence
is the whole real line and the given sequence converges there to the
function
Is this convergence uniform? We look at the difference. For a fixed k one gets
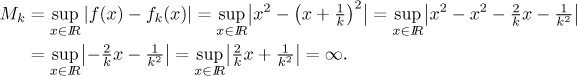
Since all suprema are infinity, there is no way they can go to zero and thus
we do not have uniform convergence on the whole real line. Obviously the
problem is that x is allowed to become arbitrarily large. Thus we
guess that we have a better chance if we investigate uniform convergence on
a closed interval
![]()
When we send k to infinity, then Mk tends to
zero, which proves that the given sequence
In fact, a similar argument shows a somewhat more general and simpler to
state fact that the convergence is uniform on every bounded subset of real
numbers.
For other examples see Solved Problems - Series of functions.
Convergence of series of functions
Back to Methods Survey - Series
of functions