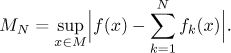
We are given a series of functions
Question 1: Investigate (pointwise) convergence and
absolute convergence of the given series of functions.
Solution: Absolute convergence:
Consider a general x from the intersection of domains, take it as a
fixed parameter and test convergence of the series of real numbers
Convergence: Consider a general x from the intersection of domains,
take it as a fixed parameter and test convergence of the series of real
numbers
Question 2: Investigate uniform convergence of the given
series of functions.
Solution:
First choose some reasonable candidate for the set of uniform convergence
M, namely some subset of the region of convergence.
In a typical case you do not get uniform convergence on the
whole region of convergence, but you can get it if you take away small
neighborhoods of endpoints of this region of convergence, often you also have
to cut away unbounded parts. Very often there is uniform convergence on any
bounded closed interval that is a subset of the region of convergence.
Having chosen one such likely set M, how do you determine uniform
convergence? In very rare cases the sum f of the series is known.
Then investigate
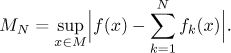
If
However, in pretty much all cases the sum f is not known. Then we most often use the Weierstrass theorem.
Weierstrass test.![]()
Step 2. Investigate the series
Remark: Sometimes one can take for ak numbers larger than the suprema in order to make investigation of the resulting series easier, see the way the Weierstrass test was stated. Note also that investigating the suprema of fk can help in guessing the right M. When we investigate suprema over the whole region of convergence and the resulting ak form a divergent series, it often helps to ask this question: Which part of the region caused these ak to be too large?
The Weierstrass test is rather powerful and it is usually the method of choice, but it is not all-powerful. Then it helps to know some alternatives, for instance the Dirichlet test or the Abel test, see Series of functions in Theory - Series of functions.
Example: Investigate convergence of
![]()
Since the number kx is positive for any real
x and any positive integer k, convergence and absolute
convergence coincide. If x is a fixed number, then we need not look
for any test, this is then a typical
Conclusion: The region of (absolute) convergence is the interval
We know that convergence of
![]()
The series
We try it again, this time with a smaller set M. We decide to test
uniform convergence for the interval
![]()
Then
![]()
and since a is chosen to be greater than 1, by the
p-test this series
converges. Thus Weierstrass's assumptions are satisfied and uniform
convergence follows.
Conclusion: The given series converges uniformly on sets
For other examples see Solved Problems - Series of functions.
Manipulating (power) series
Back to Methods Survey - Series
of functions