
Given a function f and a center a, we want to expand f into a power series with this center.
We do it by applying various transformations to series that we already know. In most cases we can do with series for the exponential, sine and cosine, and the geometric series, so you should memorize them.

Sometimes one can also use the binomial series and perhaps some series for logarithm.

The basic tool is substitution.

This is used very often, for this reason we used y in the above
expansions. The validity of a new expansion is determined easily by applying
the corresponding restriction on y to the substituted expression
Another popular modification to the above expansions is multiplication
by a power of
It is obvious that if we want to obtain a power series with center a,
then y has to feature exactly this term
How to expand.
Step 1. Identify which series will be the basis for your expansion,
keeping in mind that substitution as above can be used as well as multiplication
by a suitable power. Form a plan.
There are three typical situations.
•• The given function is essentially one of the functions whose
expansion you already know, with minor modifications. Then it is just a
question of rewriting the given function to a suitable form as explained in
Step 2.
•• The given function consists of functions whose expansions you already
know (with minor modifications) put together by operations. Unless some
trick can be used, this means that you have to expand each of these functions
and then put the resulting series together. This can be a problem, for
typical situations see
this note.
•• The given function has parts that cannot be handled by the above
approaches. Then you have to look for some trick. Very often you can use
properties of power series, namely facts about differentiating or
integrating series. If you differentiate or integrate the given function (or
its troublesome part), do you get something that you can already expand
(with modifications as above)? If this is true, use this known expansion and
then reverse the operation that got you there (see
Example below). This is
most often used to handle expansions of logarithm or expressions like
Step 2. After Step 1 it is known which function will be used as the
basis for expansion, but before expanding, rewrite the given function so that
all x in it appear in the form
Usually some unwanted parts are created during this
procedure; get rid of them using algebra and identities so that when it
comes to expanding, you can get to known expansions using substitution.
Then apply the expansion(s).
Typical situations can be found in these
examples which also serve to
illustrate the next steps.
Students usually find expansions using geometric series to be the most
troublesome. The above
example shows how one should
proceed. First, create the term with appropriate center. Then rewrite the
expression so that the constant in the denominator is in front and there is
minus after it. Finally, factor out this constant. Note also how we created
the right center for the polynomial
Step 3. Polish up the answer so that at the end there is just one
power series.
This usually means moving constants A from substitution
out of terms
Step 4. Determine the region where the resulting expansion is valid.
This is determined in the step where a series appeared in our calculations.
That step was valid only for certain values of y, from which one
easily finds restriction on x.
We will now show an example, it will be a bit longer to showcase many possible procedures (some of them less pleasant). For other examples see Solved Problems - Series of functions.
Example: Expand into a series with center
![]()
What is the plan?
Obviously, we will have to expand logarithm into a series with terms
Having expanded the logarithm, it remains to somehow involve the division by
x. There are essentially two possibilities. One is to take the given
expression as a product of logarithm and
First we will expand the logarithm. We start with expansion of its derivative.

There are two ways to get to logarithm from
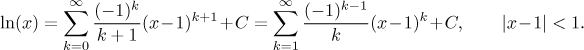
We shifted index up by 1 (the "new" k is given by
Now it is time to factor in the division by x. First the product of
series approach. We are actually lucky and save time, since we already know
how to expand

This is a typical result that comes out of the Cauchy product. Do we know some formula for the partial sum of the harmonic series, so that we could write the coefficients in the answer somehow better? Not really, so we leave it as it is. Now for the second approach.
The polynomial x has
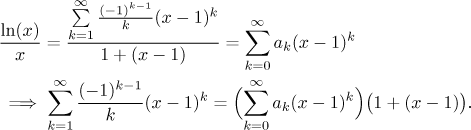
Usually we would need to use the Cauchy product on the right, but here we can actually just simplify it and express it as one power series.
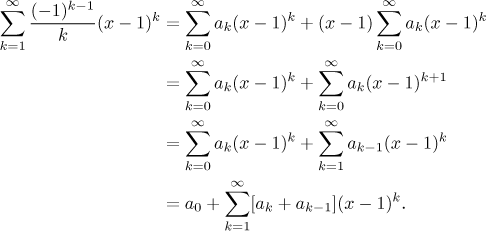
Now we have two series that are equal, so by uniqueness of expansion, their coefficients must match. We get the system of equations
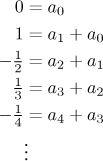
Thus we obtain
Summing up function series
Back to Methods Survey - Series
of functions