Definition.
By a power series with center a we mean any series of the form
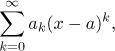
where ak are real numbers.
Power series are natural generalizations of Taylor polynomials. We know that Taylor polynomials give (if we get lucky) approximations of functions that get better as polynomials get longer, so one can expect that infinite polynomials give precisely the functions from which they arise. Before we get to this relationship, we will explore power series as such, that is, we will try to make some sense of "infinite polynomials"; they have interesting and useful properties.
Definition.
By a power series with center a we mean any series of the form
where ak are real numbers.
A very important and useful concept is complex power series, which is beyond the scope of Math Tutor; however, note that most conclusions of this section are valid also in the complex case. We will actually below sometimes refer to complex series, since some notions are somewhat more clear in more dimensional cases.
Note that an ordinary polynomial can be also considered a power series. For
instance, the polynomial
Back to power series. The basic notion - the region of convergence - behaves very nicely for power series. While for a general series of functions the region of convergence may be weird, here we know for sure that this set is the nicest possible - an interval (a circle in complex plane, a ball in general). We start with the following observation.
Fact.
Consider a power series with center a. If there exists x0 such that the given series converges at x0, then this series converges absolutely at all x satisfying
|x − a| < |x0 − a|.
Here it is exactly the case where considering complex numbers (or points from the plane) might help in understanding what is happening. If we have convergence at some point x0, then we get absolute convergence on the interior of the disc with center a on whose circumference x0 lies.

To put it another way, the series necessarily converges on the neighborhood
Note that every power series converges at its center a. The above Fact shows that if we can move further from a (away from the center) with convergence, then we also automatically extend absolute convergence. There are three possible situations. One is that there is no convergence apart from the center a. This can indeed happen. Another situation is that we can "extend" convergence as far as we want from a, that is, we get convergence everywhere, consequently also absolute convergence everywhere. The third situation is that we "extend" convergence as far as possible from a, but we cannot go arbitrarily far, there is some limit beyond which we cannot go further. Then we obtain a neighborhood (a disc in the complex or planar case, a symmetric interval about a in the real case) such that the series converges absolutely inside and diverges outside (if we had but one convergent point outside, the by the above Fact we can enlarge this neighborhood of convergence accordingly).
Thus we have the following statement.
Theorem.
Consider a power series with center a. There exists a numberR ≥ 0 (includingR = ∞ ) such that the given series converges absolutely at all x satisfying|x − a| < R and diverges at all x satisfying|x − a| > R .
This number can be found as
These formulas also include the cases
Definition.
Consider a power series with center a. The number R from the above theorem is called the radius of convergence of this series.
The theorem (including the formulas) was obtained in the following way. We
tested the given power series for absolute convergence using suitable tests
and it turned out that convergence depends on the distance from the center
Example: Investigate convergence of the series
![]()
We will use the
Ratio test
to investigate absolute convergence of this series.
Note: We will use Ak to denote terms of the series
in the Ratio test, since the traditional ak is in
the context of power series used just for coefficients, not for whole terms
of series.

(Note that in the last step we did the limit with respect to k,
x is some fixed parameter here.)
The test now shows that the investigated series converges absolutely if
What can we say about convergence at the endpoints? This has to be investigated individually, note that the Ratio test above gives lambda equal to 1 when x is from the border of the region of convergence, so it does not help.
![]()
This is the harmonic series that is known to diverge.
![]()
This is the alternating version of the harmonic series and by the Alternating series test it converges, see Convergence of general series in Theory - Testing convergence.
Conclusion: This series converges on the region of convergence
Remark: How do we know that we do not have absolute convergence at 2?
Note that if we take the series we obtained with
This means that either we have absolute convergence at both endpoints (then we also must have convergence there), or we do not have absolute convergence at any of them. From practical point of view, unless we have convergence at both endpoints, we never include endpoints in the region of absolute convergence. We will return to this below.
Example: Investigate convergence of the series
![]()
We will use the Ratio test to investigate absolute convergence of this series.
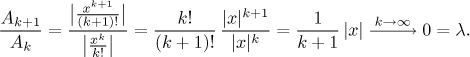
The test says that the investigated series converges absolutely if
lambda is less than 1, but we see that this happens always, regardless of
x. Thus we have
Example: Investigate convergence of the series
![]()
We will use the Root test to investigate absolute convergence of this series.
![]()
The test says that the investigated series converges absolutely if
rho is less than 1, but we see that this happens only if
Remark: The given series does not satisfy the definition of power series, but it can be rewritten into one.
![]()
Now we see that its center is indeed
We see that the three cases discussed above
(R positive,
Recall the Fact above that essentially says that if we have convergence at some point, then we gain convergence everywhere inside the disc up to that point (see again the picture above for the complex case, it is very instructive). Using this we concluded that the region of convergence is shaped as a disc. Assume now that we have a series with a positive (in particular finite) radius of convergence. Then the Fact (or the Theorem on radius of convergence) does not allow us to say anything about convergence on the circumference of the disc of convergence. And with a good reason, typically we have convergence at some places and divergence at other places of the circumference, sometimes it is just divergence everywhere or convergence everywhere. We will now show that the Fact we discuss can be strengthened if convergence at that special point is "better".
Fact.
Consider a power series with center a. If there exists x0 such that the given series converges absolutely at x0, then this series converges absolutely at all x satisfying
|x − a| ≤ |x0 − a|.
In particular, if we actually have absolute convergence at some point on the circumference of the disc of convergence, then we have convergence on the whole circumference.
Algebraic operations with series are defined in the natural way, using the definition for series of numbers, but due to their form we can only join series with a common center. An important fact is that adding/multiplying convergent power series does not spoil convergence (for the Cauchy product it follows from absolute convergence which we do have automatically for power series). Moreover, the sums of such series are what they should be.
Theorem.
Consider power series
with radii of convergence
R f andRg, respectively. Then the following are true.(i) The sum of these series converges with radius of convergence
R ≥ min(R f ,Rg) and
(ii) For a real number c, the c-multiple of a series converges with the same radius of convergence and
(iii) The Cauchy product of these series converges with radius of convergence
R ≥ min(R f ,Rg) and
We note that if in the part (i) the radii Rf and Rg are distinct, then necessarily R is equal to their minimum, see this problem in Solved Problems - Series of functions. The formula for the Cauchy product is entirely natural, we just write it in the long way and all is clear, for simplicity we use the center 0.
This theorem has an interesting interpretation. Fix some center a,
consider the set S of all sequences
then this transformation is linear. In other words, instead of functions
(which are sometimes rather complicated structures to work with) we can work
with sequences that represent them and the correspondence is best possible,
it also includes the usual linear operations. Thus from the algebraic point
of view these spaces are the same. (Here we actually also need to know that
this transformation is
How does the third statement fit in? If a function f is coded by the
sequence
The above theorem can be symbolically expressed as follows: If we introduce
the correspondence
cf ∼ c{ak},
f + g ∼ {ak} + {bk},
f⋅g ∼ {ak}*{bk}.
One can also make formulas for some other things that we do with functions, for instance substitution (division is actually quite tricky, by the way), but that is more related to expansion of functions that is covered in the next section.
An important factor when working with series of functions is the question of uniform convergence. Here the situation is pretty much the best possible. We just need to avoid the border and we are fine.
Theorem.
Consider a power series with center a and radius of convergenceR > 0. Then for every positiver < R this series is uniformly convergent on[a − r,a + r].
More generally, such a power series converges uniformly on any closed
interval that is a subset of
As usual, if we use the language of neighborhoods: "A power series converges uniformly on any closed neighborhood that is included in the region of convergence," we get a statement that is true also in other settings (complex series etc.).
This theorem is even better than it seems at the first sight. Note that we
get uniform convergence as close to the border as we want. If we take any
x0 from
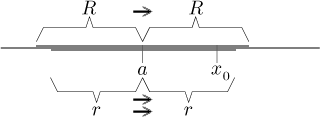
In short, we get uniform convergence around all points inside the region of convergence, so we can use all the nice properties that we had for uniform convergence (see the Series of functions) everywhere in the region of convergence. Thus we get the following extremely useful theorem.
Theorem.
Consider a power series with center a and radius of convergenceR > 0. Let f be the function that it defines on its region of convergence.
(i) The function f is continuous onUR(a) = (a − R,a + R).
(ii) The function f is differentiable onUR(a) = (a − R,a + R), on this set
and the convergence of this series is uniform on
[a − r,a + r] for any positive r < R.
(iii) The function f is integrable onUR(a) = (a − R,a + R), on this set it has an antiderivative
and the convergence of this series is uniform on
[a − r,a + r] for any positive r < R.
One can also say it like this. Given a power series, we can differentiate it term by term and integrate it term by term and the radius of convergence stays the same, convergence stays nice and the results are logical: When we differentiate a series term by term, we get the same thing as if we differentiated the function that the series defines (analogous statement is also true for integration). The fact that power series can be easily and reliably differentiated and integrated is one of the major reasons why they are so useful and popular.
Note two things. First, in the last expression on the right in (ii) we
actually dropped the first term in the indexing. It is not necessary, since
when
Second, the series that we get after differentiating and integrating are not in their proper forms, for that we would have to do a shift in indexing.
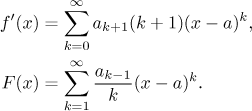
Again, depending on situation, sometimes this is done (for instance if you want to present the result in a nice polished up way), but in practice people often do not bother.
Remark: The above theorem allows us to differentiate and integrate
power series only inside their regions of convergence - and with good
reason. If a power series also converges at some border point of its region
of convergence, then this convergence need not survive differentiation and
integration. For an example consider the
first example above, the series
there was found to be convergent on the interval
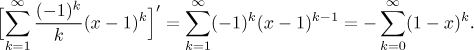
It is easy to check that the resulting series does not converge at 2.
By iterating the above theorem we find that power series yield functions that have derivatives of all orders.
Corollary.
Consider a power series with center a and radius of convergenceR > 0. Let f be the function that it defines on its region of convergence. Then for every natural number n, the function f has then-th derivative onUR(a), on this set
and the convergence of this series is uniform on
Ur(a) for any positiver < R.
Now imagine that you have two series with center a that converge and
their sums are equal on some neighborhood of a. We write this equality
of series and then differentiate n times on each side, we get on the
left and on the right expressions as in the Corollary. When we
substitute
Corollary (uniqueness).
Consider two power series with center a, a series∑ ak(x − a)k and a series∑ bk(x − a)k such that they both converge on someUr(a) for a positive radius r.
If the sums of the two series are equal on this neighborhood, then the series are necessarily the same, that is,ak = bk for all k.
This in particular means that a power series is entirely given by its values on some neighborhood of a, even very small. Once we know the values of it on some tiny neighborhood of a, then also values at other points of convergence are determined, even if the series converges everywhere.
In particular, when we have a polynomial, then it is not possible to write it in another way, not even as a truly infinite power series (with the same center, of course; if we choose a different center, we get a different expression for the same function).
A note on endpoints: We remarked that convergence of a series at endpoints need not survive differentiation, so no general statement concerning endpoints was possible in the second and the third part in the above theorem. However, the first statement (the one about continuity) is not the best possible. It can be improved, which is something that we do not get automatically from uniform convergence, but we have a special theorem about it.
Theorem (Abel's convergence theorem).
Consider a power series with center a and radius of convergenceR > 0. Let f be the function that this series defines on its region of convergence.
• If the series converges ata + R, then f is continuous there from the left and the series converges uniformly also on the interval[a,a + R].
• If the series converges ata − R, then f is continuous there from the right and the series converges uniformly also on the interval[a − R,a].
This can be summed up like this.
Assume that a power series with center a and radius of convergence
R > 0 converges on an interval I (so the interval I surely contains(a − R,a + R), but it may also include one or both its endpoints). Then the resulting function f is continuous on I and the convergence of this series is uniform on any closed interval J that is a subset of I.
In particular, if I is closed, that is, if the given power series
actually converges on
Taylor series, expanding functions
Back to Theory - Series of functions