Taylor series for the exponential

We first derive the Taylor series for f (x) = e^x with center a = 0.
Since for every natural number k, the k-th derivative is f ^(k)(x) = e^x, the coefficients are

Therefore the Taylor series is

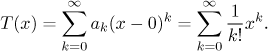
Now take any real number x. We will use the Lagrange estimate of the remainder to prove that this Taylor series converges to the exponential at this x. If we denote by I the closed interval with endpoints 0 and x, we have the estimate

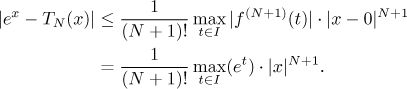
Now we need to ask where x is. If x = 0, then T(0) = 1 = e⁰. If x < 0, then the interval I is [x,0], and since exponential is an increasing function, the maximum happens at 0 and has value e⁰ = 1. Therefore

We used the fact that factorial grows faster than geometric sequence at infinity, see the scale of powers. So for negative x we have the convergence of T(x) to e^x proven.

When x > 0, then the interval I is [0,x] and the maximum of the increasing exponential is attained at x. Therefore

So also for positive x we have the convergence.

Note that if we fix some interval [−A,A], then we get a common error estimate for all x from this interval.

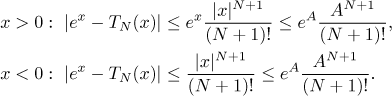
By the same argument as above, this error estimate goes to 0 as N goes to infinity, which proves that the Taylor series for exponential converges uniformly to e^x on [−A,A].