Taylor polynomial

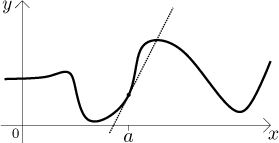
In the previous section we talked about approximating functions by tangent lines. While this is certainly useful, there is a little problem. Consider the following picture.

While the tangent line approximates the function nicely close to a, the error quickly grows when we move a bit away. The reason for this is obvious, the function curves while the tangent line does not. We would definitely get better results if we tried to approximate by some function that also curves. The second simplest function (after a straight line) is a quadratic polynomial that gives parabolas. Indeed, it seems in the picture that we would do much better with a parabola:

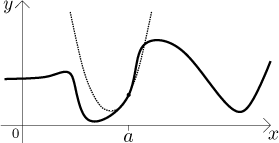
How do we find the best fitting parabola? We have to look closer at the requirements for the tangent line. There we had two. First, the tangent line had to go through the given point. Second, it had to "hug" the curve, in other words, it had to have the same direction as the function at the point a. Thus we actually wanted that the tangent line and the function have the same value and derivative at a. We then obtained the formula for the tangent line, we rearrange it a bit to fit better our purpose.

To get the best fitting parabola we obviously keep these two requirements and add another one, it makes sense to ask that the parabola also curves the same way as f at a, that is, now we also want equality of the second derivative. A little analysis shows that the parabola that satisfies these three requirements is given by the formula

Parabola approximated better, but it is obvious from the picture that a cubic curve could do even better and we do not complicate things much, polynomials are easiest functions to work with.

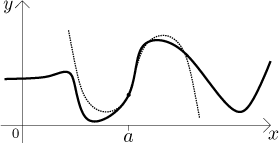
The best fitting cubic curve satisfies the same conditions as the parabola but also has the same third derivative at a as f, it is given by

Most of the pattern is now clear. Of course, there is no reason to stop at degree three, polynomials are wonderful functions and we can try increasing the degree of the approximating polynomial until we are satisfied.

Definition.
Let a function f has all derivatives up to order n at a. Then we define the Taylor polynomial of f of degree n with center a as

Note that the first two terms also conform to the pattern with derivative and factorials that we have in the sum, for instance f (a) can be written as [f ⁽⁰⁾(a)/0!]⋅(x − a)⁰.

Theorem.
Let a function f has all derivatives up to order n at a, let T be the Taylor polynomial of f of degree n with center a. Then T satisfies

T(a) = f (a),   T ′(a) = f ′(a),  T ′′(a) = f ′′(a), . . . , T ⁽ⁿ⁾(a) = f ⁽ⁿ⁾(a),

and it is the only polynomial of degree at most n with this property.

Assume that we want to approximate a function f by a polynomial p (for some possible reasons for it see below). As we saw above, the conditions p(a) = f (a), p ′(a) = f ′(a), p ′′(a) = f ′′(a) etc. come naturally. Now a general polynomial of degree n has n + 1 unknown coefficients, while the above equalities of derivatives supply us with n + 1 equations. This means that we can solve for the unknown coefficients and we get exactly those that we have in the definition of the Taylor polynomial.

Example: Consider the function f (x) = . Find its second degree Taylor polynomial at a = 4. Use it to approximate the root of 5.

Solution: To create T₂ we need the first two derivatives of f, then we need to substitute a into them.

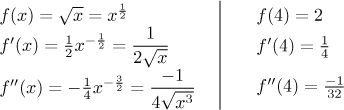
Now we create the Taylor polynomial.

It remains to estimate the root of 5.

Note that we did not multiply out the Taylor polynomial above. It is traditional to keep the Taylor polynomial in this way, since then we can see what is the reference point a for the Taylor polynomial. Note that a does not appear in the notation anywhere else. Some authors do not like this and use the notation T_a,n. We chose to follow the other convention, since it is easier and as we saw, the center is obvious from the polynomial if we keep it in the proper way.

There is another reason for keeping the terms (x − a) in the polynomial. Everything we do is related to the center a. When we substitute some number x into a Taylor polynomial, the number x by itself does not say much. Much more important is how far is x from a, in particular it influences the quality of approximation. Which brings us to the question of the error of approximation.

Definition.
Let a function f has all derivatives up to order n at a. Consider the Taylor polynomial T of a function f of degree n with center a. We define the remainder as

R_n(x) = f (x) − T_n(x).

We have a theorem that specifies this remainder. The formulation will be a bit unusual, since in general we do not know whether x is less then or greater than a.

The first result is called the integral form of the remainder, the second is called the Lagrange form of remainder. In fact, these precise results are also not exactly useful, since the integral may easily be too difficult to evaluate, while the second statement is existential, we know that such a c exists, but we have no idea what it is. However, the Lagrange form can be approximated from above and with a bit of luck it turns out that the upper estimate is small. We will return to the example above.

Example: Estimate the error we made in estimating the root of 5 above.

Solution: We used T₂ to approximate, so we need to estimate R₂(5). By Lagrange's form of the remainder there is some c between 4 and 5 such that

When estimating f ′′′(c) from above we used the fact that c is from the interval (4,5), so in particular c > 4. We see that the error we made when we approximated the root of 5 by T₂(5) was at most 1/512 = 0.002... Thus we can write

For many nice functions this maximum does not grow too fast, so when divided by factorial, it goes to zero as n→∞. This means that for a given x we can get arbitrarily precise approximation using Taylor's polynomial, we just have to take high enough order (in other words, make the polynomial long enough). For instance, all derivatives of sine and cosine are bounded by 1, so these two functions can be definitely approximated well by Taylor's polynomials. Also the exponential e^x (see this note) and the logarithm (see this note) have nice approximations.

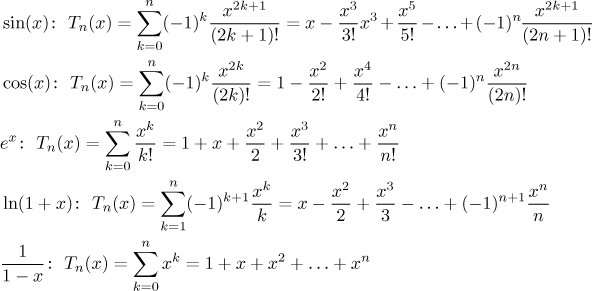
As these polynomials show, we most often take a = 0, since then we get nice simple powers. In fact, such Taylor polynomials are so useful that some authors give them a special name, they call them Maclaurin's polynomials. But sometimes other centers are nice, too. For instance, for logarithm we sometimes use a = 1:

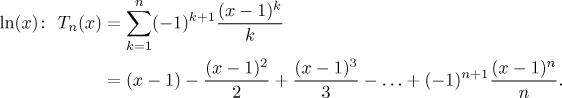
To give you some idea how this works we will now show the first few Taylor polynomials for sine and cosine. Note that polynomials for the sine do not feature even powers. This is no accident, odd functions always have Taylor polynomials with just odd powers. Thus in particular T₂ is the same as T₁, T₄ is the same as T₃, etc., so we need not draw Taylor polynomials of even degree. Similarly we will only draw polynomials of even degrees for cosine. Note how by increasing the degree we enlarge the set where the approximation is quite good.

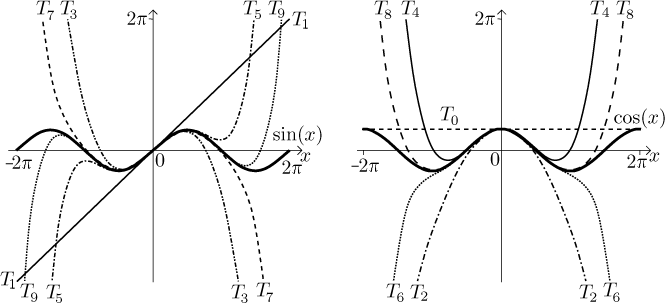
We get a good approximation for even very large parts of sine and cosine by taking Taylor polynomials of large enough degrees. It works similarly for the exponential. However, it would be a mistake to believe that this is some rule and one can rely on it. In the next picture we show the first few polynomials for ln(x + 1).

Here the quality of approximation seems to improve on the interval (−1,1), but for x > 1 it looks quite bad, as if the polynomials actually got further from this logarithm for high degrees. This is in fact true, in the section on Taylor series in Series - Theory - Series of functions we prove that those Taylor polynomials are useful as approximations of logarithm only on (−1,1].

For a brief overview and a few more examples see Taylor polynomial in Methods Survey - Applications, examples are also in Solved Problems - Applications.

To round up our exposition we will state formally the property of even/odd functions that we hinted on above.

Why do we talk about approximations? Functions with more complicated formulas can be difficult to handle and often it is possible to approximate them by something nicer under controlled conditions. Thus one can sometimes replace functions by their approximating polynomials for instance in limits or in integrals. While Taylor polynomials are definitely important in theoretical considerations, perhaps the most obvious need is when it comes to actual evaluation.

Operations that we (humans) can do are limited to addition, subtraction, multiplication and division. How do we know then what is, say, sin(2)? How about ln(3), e^1.5, 3^0.13 or root of 5? These numbers cannot be calculated precisely using just the four algebraic operations, yet people needed things like that for hundreds of years. The obvious idea is to replace the intractable functions with formulas that feature only the four operations that we can do, that is, with polynomials. This cannot be done exactly, but that is no problem since in practice we only work within a certain (known) precision. The Taylor polynomial is then a way to evaluate something that we could not do otherwise. For hundreds of years people called "computers" sat in their rooms and filled sheets upon sheets of paper with long and boring calculations, providing us with charts of values of elementary functions. Scientific (and engineering) calculations thus tended to be long and heavily dependent on good approximations, any competent engineer knew lots of them by heart.

The rise of programmable computers (e.g. calculators) hid this from a casual user, but in fact the problem remains the same, since a computer's processor can only do the same algebraic operations as human computer's brain. When we press the button labeled "ln" on a calculator, a lot of things happen, namely the calculator quickly evaluates an approximating algorithm. While Taylor polynomials are a good start, they tend to require many operations. This is unpleasant, and was more so in the days of human computers. A lot of research went into the ways of the "fastest" (in the sense "requiring the least number of operations") approximations and the results came handy when people started designing calculators.

We conclude this section with the following observation. Consider a function f that has all derivatives everywhere, fix a point a. Now we can create Taylor polynomials with this center of every degree. Assume that the function is "nice" in the sense that for every x the remainder goes to zero as we just discussed. This means that for every x we can approximate f (x) with arbitrary precision using these Taylor polynomials, we simply take long enough polynomial. It seems that things are nice, but there is a little problem. There is no universal degree of T_n that would work well for all numbers x. The further x is from a, the longer the polynomial must be to get a specific precision, and if we fix a specific precision and start moving x to infinity, then the degrees of necessary polynomials also go to infinity. This is sometimes a rather serious problem. The solution suggests itself: We take "infinite polynomials". Is there such a thing at all? The answer is positive, but it requires quite a bit of theory, in fact this has its own chapter here in Math Tutor. For "infinite Taylor polynomials" see Taylor series in Series - Theory - Power series. We also talk more there about some applications of Taylor polynomials.

Back to Theory - Applications