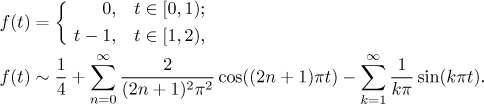
We found the following Fourier series (for periodic extension):
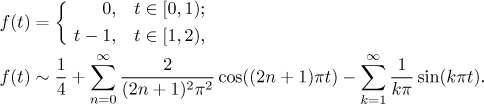
Trigonometric polynomials of the first five degrees are
We now visualize them to show how partial sums of the Fourier series adjust to the periodic extension of the given function.
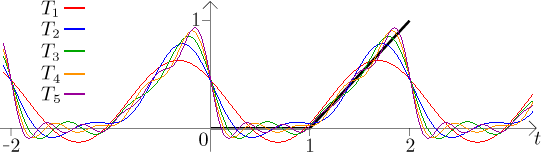
To see what is happening for longer partial sums, we will now focus on the
basic period, that is, on the interval
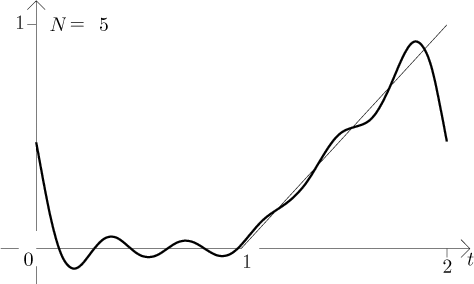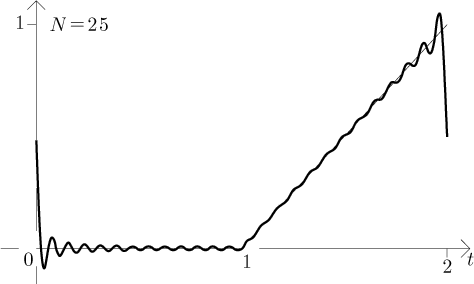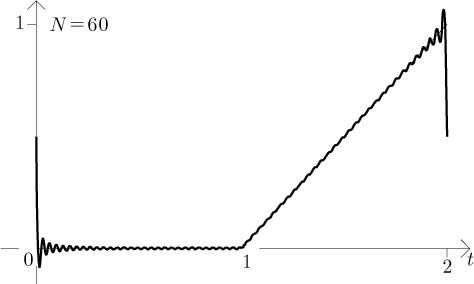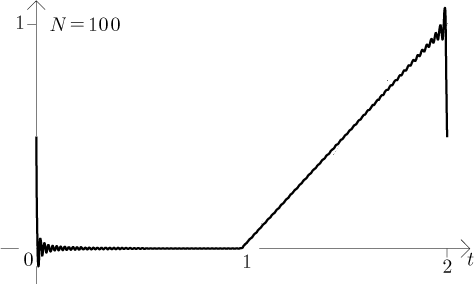
Thus the series behaves as one can expect based on Jordan conditions, in particular we see that it goes to the average at points of discontinuity. Notice the oscillation around discontinuities. As the degree of the trigonometric polynomial grows, these oscillations are limited to narrower areas around discontinuities, but the magnitude of these oscillations does not get smaller. This is called the Gibbs phenomenon and it necessarily happens when we try to approximate discontinuous functions using Fourier series.
Recall that we also found the sine Fourier and the cosine Fourier series.
Thus we have three possible series, their
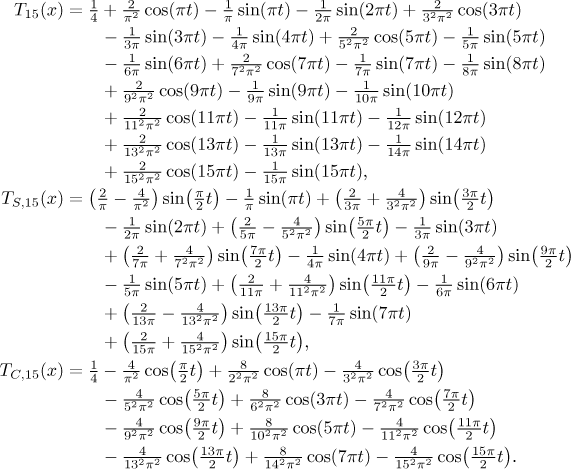
We know that the sine Fourier series converges to the odd periodic extension
and the cosine Fourier series converges to the even periodic extension (and
averages at points of discontinuity). The following picture shows that in
our example the
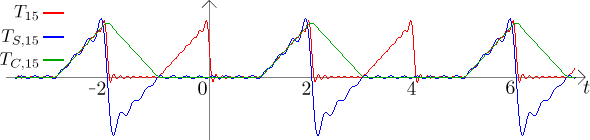
We again focus on
At the first sight this is a bit surprising. Since the sine and cosine series have fewer functions to work with, one would expect that it is harder for them to achieve good approximation, that is, one would expect them to converge slower than the "real" Fourier series. This seems to be true for the sine Fourier series, but the cosine Fourier series looks surprisingly well. Here is the reason. Note that the even periodic extension of the given function series is a continuous function, so the cosine series - while it has less functions available - has a much simpler task, since it does not have to cope with discontinuities. This agrees with theory, we know that for continuous functions (and piecewise continuously differentiable) we get a much better convergence (it is actually uniform).