Here we briefly recall basic notions related to sets. Since this section only aims to fix notation, we will not be very rigorous here.
By a set we usually mean a group of some objects. We use lower-case letters
to denote elements of sets and upper-case letters for sets. If an element
a belongs to a set A, we denote it by
We always work within a certain framework, especially if we have more sets, then we need to know what is the universe of points from which we draw elements of our sets. We usually denote this universe U. A typical set in such a universe is given by some condition, then the set is all points from this universe that satisfy the given condition. If the condition is φ with values true/false, then such a set is denoted by
Example: In the universe U of all people, the set of males would be denoted by
Note that this intuitive approach might be enough for everyday work, but involves some big problems (see this note). Thus when working more seriously with sets, the notion of a set must be done in a more complicated way. However, it will not bother us here.
Before we move on, recall that there is one special set that works in all
universes, namely the empty set
Comparison of sets.
Two sets are equal if they have the same elements. We use the usual equality
sign for it,
Consider sets A and B in a universe U. We say that
A is a subset of B, denoted
Note that this also allows for the sets being equal. By the way, the empty set is a subset of any set.
The relation of being a subset is called inclusion. If two sets are mutually included, then they must be necessarily equal.
Operations with sets.
Complement. Given a set A in a universe U, we define its complement as
Note that the notion of complement depends on the universe where we work. This is not so crucial with other operations reviewed below.
Union. Given sets A and B in a universe U, we define their union as
Note that if A and B are finite sets, that is, sets with finite
number of elements, then also their union is a finite set, but its number of
elements is not necessarily sum of the individual sizes. This is caused by
the fact that by definition, a set contains each of its elements only once,
so if we add another copy, it sort of merges with the element that is already
there. For instance, the set
Intersection. Given sets A and B in a universe U, we define their intersection as
If the intersection of two sets is empty, we say that they are disjoint.
If the sets A and B have finitely many elements, we have this interesting formula about sizes of sets (think about it, it is just a common sense):
Difference. Given sets A and B in a universe U, we define their difference as
Note that this makes sense not only when B is a subset of A but
also in general. Intuitively, the set B "takes a bite" out of
A, so parts of B that are outside of A do not do
anything. In the extreme case, when B and A are disjoint, the
difference
Symmetric difference. Given sets A and B in a universe U, we define their symmetric difference as
Venn diagrams.
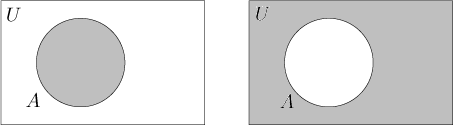
To help us in working with sets we use Venn diagrams. Traditional Venn diagrams are circles that represent sets, positioned inside a rectangle that represents the universe. There are essentially two kinds of diagrams. Sometimes we use them to show a concrete situation. For instance, in the next picture, on the left we have a set A and on the right we show its complement Ac.

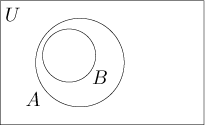
In the next picture we show the situation when B is a subset of A.
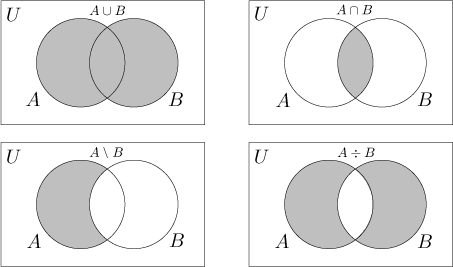
But more often we use these diagrams to think of various problems. Then we need pictures to capture the general situation; in other words, in the picture there should be places for all possible elements in relation with sets. If we have two sets, then there should be a place for elements that are in both sets, then places for elements that lie only in each set, and finally a place for elements that are not in any of the sets.

In the following pictures we indicate the operations we covered above.
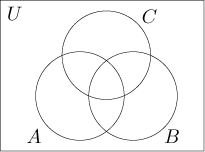
For three sets we need a different picture.
It is not possible to form a traditional Venn diagram for four sets. No matter how we put four circles in a picture, there will always be elements that cannot be put in the picture. For instance, if we try this picture,
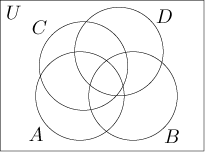
then we cannot indicate points that lie in A and D but not in B nor in C.
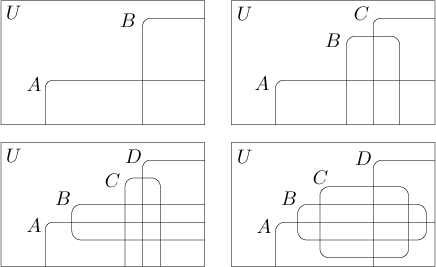
If we replace circles with rectangles, then we can go to four sets, as an added bonus the diagrams now look cooler and modern. The fourth picture shows a modification of the picture with four sets, we can similarly modify the picture with three sets.
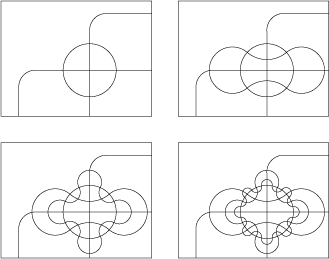
People tried to come up with ways to show more sets, as an example we show Edwards diagrams for three to six sets.
We can mark elements of a set in a Venn diagram. The set

If a set is ordered, we also use this picture:
![]()
We often use this kind of a picture for infinite sets of numbers, for instance integers.
Consider sets A and B. We define their Cartesian product as the set
Example: Consider sets
We can draw such a Cartesian product like this:

For instance, the upper right dot represents the couple