Long division and the "add-substract" trick

Dividing polynomials with remainder is one of the basic algebraic skills and here in calculus we use it mainly when decomposing to partial fractions. We will explain this algorithm on a suitable example.

Problem: We divide with remainder

• First divide the leading term (the one with the highest power) of the numerator by the leading term of the denominator. In our case we get 2x³ : x² = 2x. This gives us the first term of the result:

  

• We use the term that we just obtained to multiply the denominator and subtract the result from the numerator:

  

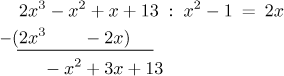
• If the remainder is of lower degree than the denominator, the calculation is done. Otherwise we go back to the beginning, divide the leading term of the remainder by the leading term of the denominator and so on.

In our example this algorithm leads to

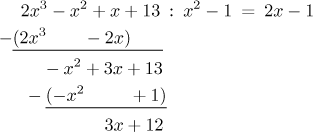
and therefore

The "add-substract" trick

It is a very general trick that is ocassionally used when manipulating algebraic expression. Often we find ourselves in position when we would really appreciate if there was a certain something in the given expression, but we do not have it there. In many cases we can simply put it there by adding, but to balance it out we have to subtract it as well.

We will show how it can apply to the example above, this time we try to divide in another way. For instance, we would really like if we had 2x³ − 2x in the numerator, so we create it there and then use it.

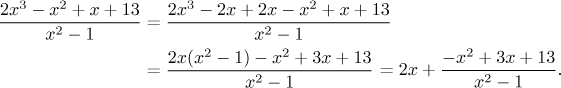
Now we would really like it if we had -x² + 1 in the numerator, so we again create it there.

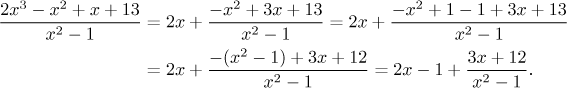
This way of dividing can be sometimes really fast and convenient.

There is a similar trick that we can call "multiply-divide". For instance, imagine that we have the expression 3x + 5, but we would prefer to have the coefficent 7 at x and do not want other terms with x there. This last requirement prevents us from adding and subtracting, but we can do this:

3x + 5 = 3⋅(x + 5/3) = (3/7)⋅(7x + 35/3).