L'Hospital's rule

This topic is actually borrowed from the theory of functions. Therefore we just briefly restate the theorem in the form applicable to sequences:

Theorem (L'Hospital's rule).
Let f and g be functions defined on some (K,∞). If both f and g have limit at infinity equal to 0, or both f and g have infinite limit at infinity, then

assuming that the limit on the right exists.

How does it help? Imagine that we have two sequences, {a_n} and {b_n}, and we are investigating the limit of their ratio. One of the most typical problems is that we get an indeterminate ratio, that is, the type or . If the formula that defines the sequence {a_n} also determines some function f and the formula that defines the sequence {b_n} also determines some function g, we can try to use the above theorem. We have to check that the functions f and g have the same limits at infinity as the given sequences (both zero or both infinity). If they do, we are exactly in the position of the above Theorem. Therefore, we can pass to investigation of functions instead of sequences and then use the l'Hospital rule.

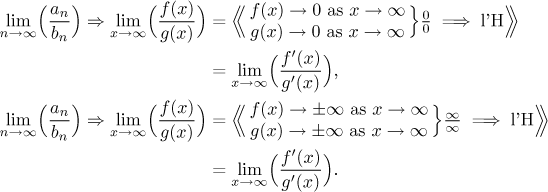
In any of the two cases above, if the limit on the right exists, then the result is also valid for the limit on the left, consequently also for the ratio of the two sequences. On the other hand, if the procedure fails (for instance if the limit on the right does not exist), we cannot say anything about the sequence problem (see for instance this example in Solved Problems - Limits).

Note that usually we would use a shorter way to indicate the application of the l'Hospital rule, see the next example.

Example:

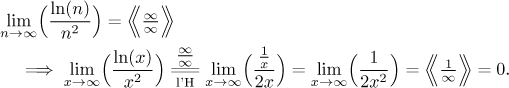
Since we got a definite answer at the end, the "conditional equality" in the l'Hospital rule step is justified.

The assumptions in the theorem as essential for its validity. If a limit is not of the specified type, l'Hospital's formula is no longer generally true. Consider the following very simple example:

Example:

Note that this limit problem was not of the l'Hospital type (zero over zero, infinity over infinity, not even something over infinity) and therefore l'Hospital's rule cannot be used. What happens if we forget to check type and get seduced by the ratio form of this problem to apply the l'Hospital rule? We get the wrong answer:

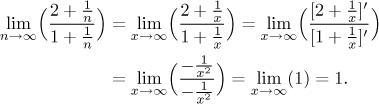
The l'Hospital theorem can be actually stated in more generality. The version that we quoted above is the one used in most calculus texts and courses. This is why we will usually (if possible) pretend while solving problems in Math Tutor that it is the only version we know, so that you won't run into trouble by getting used to something your prof did not cover.

What is the more general version? The case cannot be generalized, there the theorem was the best possible. However, for the other case, , we actually need not worry about the numerator; the l'Hospital rule applies to the type "something over infinity"!

Does this more general version have any advantage? Consider the ratio a_n /b_n with b_n→∞. What can happen with the numerator? If it also goes to infinity, then we can use the first, more popular version; thus this new one is no improvement. If a_n converges to some real number A, then the whole ratio converges to A/∞ = 0, so we know the answer without l'Hospital.

You can see that in most cases, the first version of l'Hospital is quite sufficient. Is there any advantage to the new version then? Definitely. First, you may encounter problems where the numerator does tend to infinity, but proving it would be so much work that you would really appreciate knowing that you can skip it and use the more general rule (you still have to prove that the denumerator goes to infinity, but that's half the work compared to the first version of l'Hospital). So the more general version is definitely more convenient for the problems with infinity (it saves no work in "zero over zero" cases).
But that is not all. It may happen that the numerator actually does not have any limit! While the first version cannot be used for the type "DNE over infinity", the more general one can! Therefore, although we promised to stick to the first version whenever possible, we will also use the more general one ocassionally.

For practical tips on l'Hospital's rule see the box "indeterminate ratio" in Methods Survey - Limit.

In Solved Problems - Limits, l'Hospital's rule is used in this problem (which is a typical textbook example), it is also a part of most other solutions, notably in this problem, this problem, this problem, and this problem. For a nice example where the l'Hospital rule can be applied, but leads to no conclusion, check out this problem.

Intuitive evaluation
Back to Theory - Limits