Box "indeterminate ratio"

The situation is as follows: We need to find the limit (if there is any) of a ratio an /bn. After evaluating individually the numerator and the denominator we found out that we are facing an indeterminate ratio, that is, the types or . What can we do? There are several alternatives.

1. L'Hospital rule

This is the standard procedure.
Step 1. From a limit of sequences we pass to a limit of functions (see Sequences and functions in Theory - Limits). This can be done assuming that an is given by some function f (n) and that bn is given by some function g(n).

Step 2. Check that the ratio f /g is still of the indeterminate type at infinity.

Step 3. Apply the l'Hospital rule:

that is, differentiate the numerator and the denominator of the fraction. Then try to find the limit of the resulting fraction; if this limit exists, it is also the answer to the original problem with sequences.
If the limit on the right does not exist, then we get no conclusion about the original sequence problem.

Example:

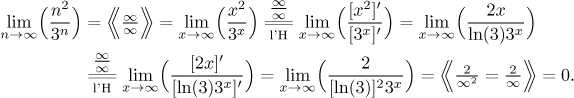
Note that we had to use the l'Hospital rule twice. This happens often, sometimes we even have to use it more times. This example was typical: We can use the l'Hospital rule to "get rid of powers", each derivative removes one power. When investigating the limit of, say, en/n13, we would have to use this rule 13 times, each time lowering the power by one until it disappears. Similarly, the l'Hospital rule can be used to get rid of powers of logarithms, one l'Hospital gets rid of one logarithm. These are the most typical applications.

Notes:
1. When applying l'Hospital's rule, we take separately the derivative of the numerator and the denominator. We do not apply the ratio rule to the whole fraction, as students are sometimes tempted to do. L'Hospital has nothing to do with taking derivative, it is a special tool for finding limits that happens to use derivatives in its own way. Of course, if the expressions in the numerator and denominator are more complicated, we use the appropriate rules when differentiating them.

2. It is crucial to check that we are facing an indeterminate ratio. L'Hospital's rule cannot be applied to other types of fractions with one exception. We can apply it if |g| tends to infinity as x goes to infinity, regardless of what f is doing. That is, in full generality, this rule applies to two types: "zero over zero" and "anything over infinity". For other types the rule does not work, see L'Hospital rule in Theory - Limits.

3. Although the l'Hospital rule works in great many cases and seems to be quite reliable, it is not a universal solution to indeterminate ratios. Sometimes it cannot be applied at all, for instance if the functions f and/or g we obtain are not differentiable; it may even happen that the formula defining an and/or bn cannot be extended to define a function! Typical examples are powers with negative bases like (−1)n, (−2)n etc. We cannot make them into functions like this: (−1)x, because exponentials are only defined for positive bases. For instance, the number (−1)x itself does not even exist when x is a fraction with an even denominator and odd numerator.

Sometimes the l'Hospital rule can be used, but fails to help, that is, we obtain a limit that does not exist or cannot be calculated, other problems can happen as well.

Finally, there are problems that l'Hospital's rule does solve, but we are better off using another approach; the most typical case would be ratios involving powers, exponentials and square roots, since exponentials do not change after differentiation and the derivative of a square root again yields a root, often a more complicate one.

Example: We will apply l'Hospital's rule to the following problem. Note that we start by rearranging the formula to get positive exponents; in this way we get a better feeling for the type. For l'Hospital calculations we then use the original form as it is easier to differentiate.

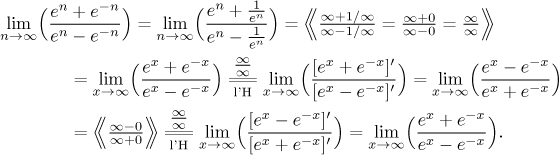
After two l'Hospitals we ended up exactly where we started, so the l'Hospital rule did not help. This is a rather curious example, as this does not happen often; yet it shows that l'Hospital can fail even for very nice examples.

Actually, an experienced student would not apply the l'Hospital rule to this problem at all. At the first glance, this problem is of the type ratio of sums of powers, that is, there should be a relatively painless solution found in the box "polynomials and ratios with powers", see below.

In short, l'Hospital is often not the best choice when the given expression features exponentials and also roots.

In Solved Problems - Limits, l'Hospital's rule is used in this problem (which is a typical textbook example), it is also a part of most other solutions, notably in this problem, this problem, this problem, and this problem. For a nice example where the l'Hospital rule can be applied, but leads to no conclusion, check out this problem.

2. Polynomials and similar terms

If the limit also falls into the box "polynomials and ratios with powers", we are usually better off using tools from that box. As an example we return to the one with exponentials above.We identify the dominant terms in the numerator and the denominator: They are the same, namely en. So we factor it out in both parts of the fraction, here it will be even easier if we simply cancel this term in both parts:

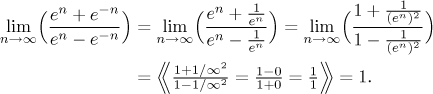
That was easy, wasn't it? As a matter of fact, we could have guessed the answer right away using intuitive evaluation. Since the terms e−n tend to zero, the trouble is really caused by the exponentials en. They are the dominant terms in both the numerator and the denominator, so the fraction behaves like en/en = 1.

This example was rather typical. While the l'Hospital rule can handle many or even most ratios that belong to the box "polynomials and ratios with powers", it is very often easier to apply the methods from that box.

3. Difference of roots

As we mentioned above, roots are sometimes quite troublesome when it comes to l'Hospital rule. If the roots are mixed up in a difference, they might be removed using the appropriate trick from the box "difference of roots".

Almost all examples in Solved Problems feature indeterminate ratios, so check them out.

Of course, there are also indeterminate ratios that can't be solved using these threer approaches and one has to handle them individually.

Next box: indeterminate product
Back to Methods Survey - Limits