Box "indeterminate power"

What do we do when we try to evaluate a limit and we end up with one of indeterminate powers 1∞, 00, ∞0?

The standard procedure is to change this power into a product using the "e to logarithm" trick. This trick is based on the fact that for every positive real number x we have x = exp(ln(x)) and on the fact that logarithm changes powers into products. Namely, we transform the power as follows:

Since this is just an algebraic transformation, the limit of the expression on the left is the same as the limit of the expression on the right. That one has the form of "e to something". Since exponential is a "nice function", we can "pull it out of the limit" and find the limit of the exponent first. This expression is a product, which is something that we know how to handle. What kind of a product is it? If we start from an indeterminate power, we always get an indeterminate product:

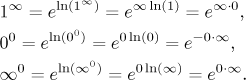
Thus we can apply the standard procedure (change the product into a ratio, pass to functions, use l'Hospital, see the box "indeterminate product"). After we find the limit of the exponent, we have to remember to put it back into the exponential.

As an example we will prove the rule for the exponential limit

We first check that the limit gives an indeterminate power, then do the "e to ln" trick:

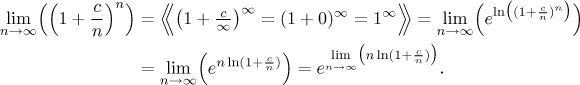
As you can see, we pulled the exponential out of the limit. Now we will try to find the limit in the exponent, and since we know that it will lead to indeterminate form, we pass to functions right away:

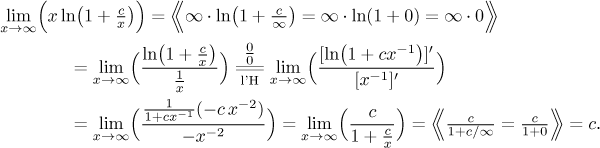
We found the limit, but now we have to remember to substitute this answer to the exponential:

Note: If we have a power and we are not sure whether it is an indeterminate form or not, we can always use the "e to ln" trick and it will tell us. For instance, if we are not sure that 0∞ = 0 (see the limit algebra), we can do

Note: An inquisitive reader should have gotten suspicious when we were transforming powers using the "e to ln" trick. Why? Because ln(0) does not exist, we cannot plug zero into logarithm. Now we know that this zero is not really a zero, it represents a sequence that converges to zero (compare this note), but this does not help very much since logarithm does not have a limit at zero!

The secret is here: we cheated a bit when writing the power. General power requires that the base be positive, so in fact we do not have 00 and 0∞, but (0+)0 and (0+)∞; that is, the base is a "positive zero", a sequence that converges to zero and has only positive terms. Consequently, in the subsequent calculations we get ln(0+) and this is already well-defined, the limit of logarithm as x goes to zero from the right is negative infinity as stated above.

Why did not we write the proper expressions (0+)0 and (0+)∞ in the list of indeterminate powers? Because nobody bothers, it looks ugly, so we did not bother either. As a matter of fact, most calculus textbooks do not even bother to caution you about this one-sided stuff, we at least warned you. The good news is that you should not get bad results anyway. You should always check on 0 when putting it into logarithm in the limit algebra, and if the zero in the power was not of the positive type, the logarithm would not exist and you would find out that there is something fishy.

In Solved Problems - Limits, these methods are used in this problem.

Next box: comparison and oscillation
Back to Methods Survey - Limits