Here we will look at some theory concerning concavity. For practical approach using derivatives see Concavity in Derivatives - Theory - Graphing functions.
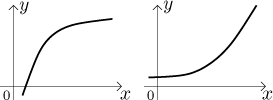
Consider a function increasing on an interval. This tells us that the function is growing, but does not tell us how, since there are many ways in which a function can grow. Of the many possibilities we chose two nicest and in some sense most typical:

The difference is important from two points of view. First of all, functions are supposed to be useful, they are used to describe things. Here we know that some quantity is growing, but in the first picture the trend is that the growth is slowing down, whereas in the second case the growth seems to be getting out of hand. Depending on the situation, one of these cases may be very bad and the other very nice. For instance, if the graph shows how much money you've got in your retirement fund over the years, the second picture would be very desirable (and is typical of ads), interest builds up over the years. On the other hand, the graph may show how much heat is generated over time by some chemical reaction you are connocting in a lab. The first picture is something you hope to see, the second picture is usually called an "explosion" and you should quickly get as far as possible.
Perhaps more importantly for a student of calculus, these two shapes are very different when it comes to drawing a graph, the first is "curving down" and the second is "curving up". These two trends are in fact independent of the function being increasing, in the following picture the first two graphs "curve down" (one is decreasing, another not monotone, an increasing curving down graph is above), then we have two graphs that "curve up" (again, one decreasing, one not monotone, and one increasing is already above).

In math lingo, if the graph of a function is "curving up" somewhere, it is called concave up, when it is "curving down" somewhere, it is called concave down. Some people actually use terminology (in the same order) convex and concave. When we are interested in such stuff, we say that we are investigating concavity of the given function.
Life being what it is, there are functions that are pretty crazy when it comes to concavity, they may change the way they go just about everywhere and no nice picture is possible (see the Dirichlet function). However, for a typical function, its graph would have parts that hold on to one of these two shapes, so it would be concave up for a while (on an interval), then concave down, then... This is exactly the situation we will try to explore. The notion is actually roughly similar to monotonicity in the way it works, as you will see, so we should start with concavity at a point. However, nobody really uses this, so we will leave it as a note at the end and go right to concavity on a set (typically an interval).
How do we express mathematically that "curving up" business in the very first picture? Let's have another look at the example on the right there. There are two ways to look at it. One is that when you go from one point to another and then try to make the next step, you have to go steeper up. Another point of view is that when you try to move from some point, the further you want to step, the steeper you must go. And of course, this should work at all places of the curve.
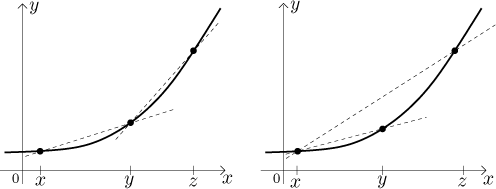
Now that steepness we talk about is actually the slopes of the lines connecting points in the picture, so what we said above translates to inequalities between slopes. Slopes are simple to find, so we get the following definition.
Definition (concavity).
Let f be a function defined on a set M.
We say that f is concave up on M if for any three pointsx < y < z∈M we have
Equivalently, f is concave up on M if for any three points
x < y < z∈M we have
We say that f is concave down on M if for any three points
x < y < z∈M we have
Equivalently, f is concave down on M if for any three points
x < y < z∈M we have
We say that a point
x∈D( f ) is an inflection point or a point of inflection if there is a left neighborhood of x on which f is concave up and a right neighborhood of x on which f is concave down, or there is a left neighborhood of x on which f is concave down and a right neighborhood of x on which f is concave up.
In short, inflection points are those where concavity changes (alternative spelling inflexion is also used). As usual, most often we explore concavity on intervals, in particular because we have some handy tools for it.
Example:
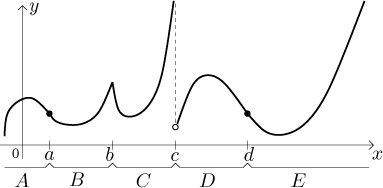
The function in this picture is concave up on intervals B, C, and E, concave down on intervals A and D, and has inflection points a and d (it changes concavity at c, but this point is not in the domain of f).
Alternative terminology: Unfortunately, here we also have an alternative terminology. Some people say convex when they mean concave up, and concave when they mean concave down. This is related to shapes of regions. The region above a graph is convex exactly if the graph is concave up, that is, "convex". It is hard to guess which of these terminologies is more spread. I have a feeling that Europeans prefer the "convex-concave" pair, whereas in America people prefer the "concave up-concave down" pair, but I might be wrong. Being European, I have been taught this alternative way, but I have to admit that the "up-down" way seems easier to remember and more intuitive, so I will stick to it in Math Tutor.
Before we go further, we will state a theorem which tells us that the picture above was not too nice, that once a function has some kind of concavity, then it cannot have unpleasant jumps and other surrises like we saw with monotonicity.
Theorem.
If a function is concave up on a given open interval or concave down on it, then it is also continuous on it.
There are alternative ways to see (and define) concavity; they should seem natural if you refer to pictures above.
We start with the first inequality in the formal definition above, the one describing concavity up using two consecutive slopes. A little algebra shows that the inequality can be written like this:
![]()
This looks rather ugly, but it gets more interesting when one notices the following. Consider this formula (with numbers x,z fixed and variable t):
![]()
In fact, it is a formula defining the line connecting the points
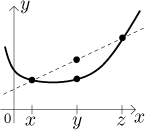
Geometrically, we are saying this: We pick two points, x and z. Then we pick some point between them, and the value of f of this point must be less than or equal to the value we would get by connecting the two chosen dots with a segment. This brings us to the following geometric definition of concavity, and since we will be only picking two points, we will rename z to y:
A function is concave up on an interval I if for every two points
A function is concave down on an interval I if for every two points
This geometric idea of concavity can be expressed in a different way. It
is well-known in mathematics that when x and y are two real
numbers, then all numbers between them can be expressed as
A function is concave up on an interval I if for every two points
![]()
A function is concave down on an interval I if for every two points
![]()
The last geometric characterization of concavity is not as universal as the above ones, since for some functions it does not work. The reason is that not every graph of a function is nice enough to have tangent lines (see tangent lines in Derivative - Theory - Applications). Assume now for a second that we have a function whose graph is so nice that at every its point we can find a tangent line.

A function is concave up on some interval exactly if whenever we draw a
tangent line at some point in this interval, then the graph (more precisely,
the part corresponding to the interval of concavity up) lies on or above this
tangent line.
A function is concave down on some interval exactly if whenever we draw a
tangent line at some point in this interval, then the part of the graph
corresponding to the interval of concavity down lies on or below this tangent
line.
An inflection point is characterized by the property that if we draw a
tangent line at this point, then there is a neighborhood so that on it the
graph lies above this tangent line to one side of the point and below on the
other side.
Remark: One can also define strict concavity by making the inequalities in the definition sharp. This is possible, but it is rarely used. One reason for defining it might be that some people feel uncomfortable with the fact that one can have functions that are simultaneously concave up and concave down. In fact all straight lines, that is, all linear functions, work this way.
Connecting intervals.
Here we will address the following situation: We know that some function
f is concave in a certain way on two intervals, I and J.
Can we say anything about concavity on their union? Unfortunately, not much
in general, situation here is much worse than with monotonicity. Just look at
the example with letters A, B, C,... We had a function
that was concave up on intervals B and C but not on their
union, even though the graph was nicely connected there, without any jumps.
There are some conditions that could be checked, but they are not very nice
and no convenient procedure exists.
In fact, the only situation when one can guarantee without further investigation that a function concave up on two intervals will be also concave up on their union is this: The intervals must overlap by more then one point. Unfortunately, such a situation pretty much never happens in applications.
Here we will do the obvious, define local concavity. The global properties should be a good enough inspiration. To make clear what we mean, we will show a few pictures of functions that are considered concave down at a given point.

Definition (local concavity).
Let f be a function defined on some neighborhood of a point a.
We say that f is concave up at a if there is a neighborhood U of a such that for any two points x,y fromU ∩ D( f ) satisfyingx < a < y we have
We say that f is concave down at a if there is a neighborhood U of a such that for any two points x,y from
U ∩ D( f ) satisfyingx < a < y we have
As you can expect, a function is concave up on an open interval exactly if it is concave up at all points of it, an analogous statement is true about concavity down. Since most textbooks don't bother even introducing this notion, we will ignore it too, this is the only time you will hear about it here in Math Tutor.