There are two ways to check continuity - global and local.
We know that great many functions are continuous on their domains, namely all elementary functions. We also know that when combining elementary functions by operations, continuity is preserved. Thus we can tell continuity of any function that is composed of elementary functions.
Example: The function
![]()
is continuous on its domain
Note that for continuity we need both-sided neighborhoods, so the above procedure gives continuity only on open sets. If the domain happens to include some of its endpoints, we only get one-sided continuity there. This may have far reaching consequences in more complicated setups (like split functions), so it is safer to use this global approach only on open sets, that is, to handle endpoints individually (see local continuity below).
Split functions. Split functions are defined by different formulas on
(typically) disjoint sets. If every formula is continuous on the set to which
it applies, then the split function is continuous on the union of
interiors of these sets. Indeed, it is important to recall that when a
function is continuous on an interval
Given a function f and a point a in its domain, we want to know whether f is continuous at a. There are two possibilities.
Case 1. There is some neighborhood U of a on which the
function is defined by some expression whose continuity we already know. Then
f is also automatically continuous at a. For instance, the
function f from the previous example is continuous at
Case 2. There is no such neighborhood. In the most typical case this
means that the function is defined in different ways to the right and to the
left of a. For instance, the absolute value
In such a case we determine continuity and classify discontinuity if it appears in the following way:
Step 1. Determine both one-sided limits at a and the number
Step 2. Compare the three numbers from Step 1 and draw conclusions.
There are these possibilities:
• The two one-sided limits converge, they are equal (so they also give the
(both-sided) limit) and they are also equal to
• The two one-sided limits converge and they are equal (so they also give
the (both-sided) limit), but not equal to
• The two one-sided limits converge, but they are not equal. Then the
(both-sided) limit does not exist, the function is not continuous at
a, it has a jump discontinuity there.
• At least one of the one-sided limits does not converge. Then the function
is not continuous at a, it has a discontinuity of the 3rd kind
there.
To decide whether a given function is continuous at a from the left,
we first evaluate its limit at a from the left and
If the limit from the left converges and is equal to
Continuity from the right is done in analogous way.
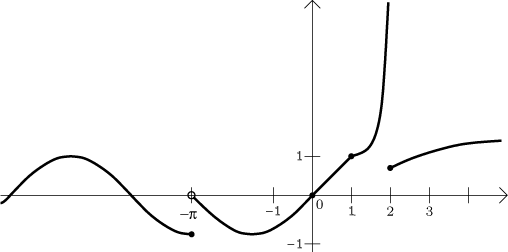
Example: Determine continuity of

Solution: We start with global continuity the easy way. For every interval specified in the definition, the function f is defined by one concrete continuous function on that interval, so it is also continuous there. Since we have to be careful and only work with open sets, we have the conclusion that the given function is continuous on the set
What about the points missing from this set? We have to use the local
approach and check on continuity at the points

Conclusions:
• At
• At
• At
• At
When we put this together with the global step, we get the
Result: f is continuous on the set
It is also continuous from the left at
The picture shows what is happening, but note that we did not need it to make our conclusions.
For more examples see Solved problems.
1-1 and inverse
Back to Methods Survey - Basic
properties of real functions