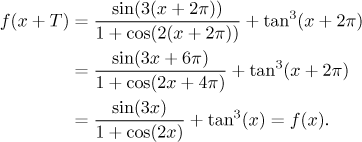Problem: Determine periodicity of the following function:
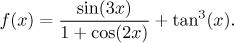
Solution: We always start by checking on the domain. Here there are
two problems. First, the tangent rules out all numbers of the form
π/2 + kπ.
We also have a fraction, the denominator cannot be zero. Thus the cosine
cannot be −1, therefore numbers (2x) cannot be
(2k + 1)π, that is,
x cannot be
π/2 + kπ.
Remarkably enough, we've got the same condition from tangent and cosine, but
that's just a happy coincidence. Thus the domain is all real numbers apart
from the type listed here.
Now back to the periodicity. The function consists of three composed
functions combined together using algebraic operations. First we look at each
composed function.
sin(3x) has periodicity (2π)/3, since it is a
2π-periodic sine whose argument was scaled (see
Methods Survey - Real functions -
Transformations).
The second function we look at is cos(2x), which is - by the same
argument -
π-periodic. We
can even include the "+ 1" part, we know that shifting a function up does not
change its period.
The third term is tan3(x). Tangent is
π-periodic and cubing it does
not change the period (when composing functions and the inner one is
periodic, the outer one does not spoil it, again see
Methods Survey - Real functions -
Transformations).
So we have three functions whose periodicity we know and they are combined
using division and addition. The rule says that in such a situation, the
outcome has period which is the least common multiple of the periods of the
individual parts. In our case we have periods
2π/3 and
π, so we are looking for a
positive real number r such that
r/(2π/3) is an
integer and
r/π is
an integer. The second condition says that
r = kπ for some positive integer
k, and the smallest k that would work for the first condition
is 2.
We therefore claim that T = 2π is a period of the given
function.
Confirmation:
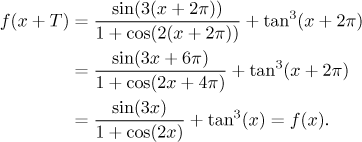
Next problem
Back to Solved Problems - Real
functions
![]()