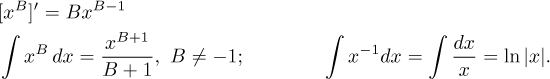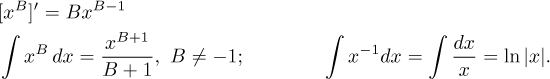Mocniny jako čísla a funkce
Začneme s následující otázkou. Máme dvě reálná čísla, A a B,
a chceme vědět, jak spočítat AB
(pokud je to vůbec možné).
Budeme tuto mocninu definovat krok za krokem v závislosti na exponentu
B, začneme jednoduchými a půjdeme k obecnému.
Případ 1. B = 0. Definujeme
A0 = 1 pro všechna reálná čísla A.
Případ 2. B = n je přirozené číslo. Definujeme
An pro všechna reálná čísla A indukcí,
A1 = A a
An+1 = A⋅An.
Jinými slovy, An je prostě
A⋅A⋅...⋅A, číslo A násobí
samo sebe n-krát.
Případ 3. B = n je celé číslo. Jestliže
n není záporné, pak už jsme to probrali předtím. Jestli je n
záporné, definujeme
An = 1/An.
V tomto případě nesmí být A nula.
Případ 4. B = 1/n, kde n je přirozené
číslo. Dá se dokázat, že jestliže
A ≥ 0, pak rovnice
xn = A má jedno řešení
x ≥ 0. Toto řešení se jmenuje
n-tá odmocnina z A a my definujeme
A1/n jako tuto odmocninu.
Pokud je navíc n liché, můžeme hledat odmocninu také pro záporné
A. Proto můžeme počítat A1/n jako
n-tou odmocninu pro všechna A, jestliže je n liché, a
pro nezáporné A, jestliže je n sudé.
Poznámka: Jestli je n sudé, pak má rovnice
xn = A dvě řešení, jedno záporné a
jedno kladné. Toto jsou řešení rovnice, jako odmocninu bereme jen to kladné.
Někoho tohle mate, ale je to v zásadě velmi jednoduché. Rovnice
x2 = 4 má dvě řešení, 2 a
−2, ale druhá odmocnina ze 4 je 2.
Případ 5. B = p/q je racionální číslo,
kde q je přirozené číslo a p je celé číslo (můžeme
předpokládat, že p není nula, protože ten případ už jsme definovali).
Teď definujeme
Ap/q = (A1/q)p,
k určení, jaká A jsou povolena, je třeba rozlišit několik případů.
Jsou dvě omezení: Za prvé, je-li p záporné, pak A nemůže být
nula. Za druhé, je-li q sudé, pak A nemůže být záporné. Jsou
tedy čtyři možnosti:
a) Je-li p kladné a q liché, pak A může být
libovolné reálné číslo.
b) Je-li p kladné a q sudé, pak vyžadujeme
A ≥ 0.
c) Je-li p záporné a q liché, pak vyžadujeme
A ≠ 0.
d) Je-li p záporné a q sudé, pak vyžadujeme
A > 0.
Případ 6. B je nějaké reálné číslo, zase budeme předpokládat,
že není nula. Zde definujeme mocninu následovně. Vybereme libovolnou
posloupnost {b(k)} racionálních čísel, která konverguje k
B (píšeme b(k) namísto
bk).
Protože nemůžeme zaručit, že všechny jmenovatelé v této posloupnosti jsou
liché, musíme se omezit na A > 0 pro B záporné a na
A ≥ 0 pro B
kladné. Pak se dá dokázat, že posloupnost
{Ab(k)} konverguje k nějakému číslu, které
nazveme AB.
Aby byla tato definice korektní, musíme dokázat tři věci. Za prvé, že
posloupnost {Ab(k)} opravdu konverguje. Za
druhé, že když vybereme jinou posloupnost {c(k)} jdoucí k
B, pak posloupnost
{Ac(k)} konverguje
k témuž číslu jako {Ab(k)}. Konečně, je třeba
dokázat, že když B padne do některého z předchozích případů (celé
číslo, racionální číslo), pak definice skrz posloupnosti souhlasí s obvyklou
definicí, jak tam byla popsána. Naštěstí se všechny tři věci dají dokázat,
takže máme mocninu.
Mocnina AB, jak jsme ji definovali, splňuje obvyklá
pravidla, která platí, kdykoliv jsou vyskytující se mocniny definované:
(A⋅B)C =
AC⋅BC,
(A/B)C =
AC/BC,
A−B = 1/AB,
AB+C =
AB⋅AC,
ABC =
(AB)C =
(AC)B.
Mocniny jako funkce
Mocniny jako funkce dostaneme, když uvažujeme mocninu
AB a necháme měnit základ A, pak dostaneme
funkci
f (x) = xB. Rádi bychom
věděli, co to znamená a jaké má vlastnosti. Jako předtím se podíváme na
několik případů podle toho, jaké je B. Začneme od nejobecnějšího
případu, kdy je B nějaké reálné číslo, a uvidíme, jaké vlastnosti
platí pro všechny mocniny. Pak se podíváme na speciálnější případy.
Obecný případ: B je reálné číslo. Když nemáme o B
nějakou speciální informaci, pak definiční obor je
(0,∞). Máme následující
vlastnosti:
• algebra: Pro všechna
x,y > 0 a libovolné reálné A,
B platí
(x⋅y)B = xB⋅yB,
(x/y)B = xB/yB,
x−B = 1/xB,
xA+B = xA⋅xB.
• srovnání: Jestliže
A < B,
pak pro všechna x > 1
platí
xA < xB.
Naopak pro
všechna x splňující
0 < x < 1 platí
xA > xB.
• spojitost: Mocniny jsou vždy spojité na jejich definičních oborech.
• derivace a integrál:
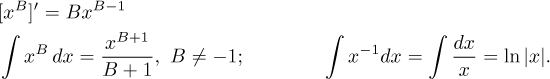
Další vlastnosti záleží na znaménku B. Jestliže
B = 0,
pak
xB = x0 = 1,
tj. máme konstantní funkci definovanou na celé reálné ose. Jestliže
B > 0, pak definiční obor
xB je vlastně
⟨0,∞),
funkce je omezená zdola
ale ne shora (proto není omezená), je rostoucí. Jestliže
B < 0, pak
často dáváme přednost zápisu
xB = 1/xB;
funkce
je omezená zdola ale ne shora (proto není omezená), je klesající.
Definiční obor této funkce lze rozšířit, pokud víme víc o B.
Jmenovitě, předpokládejme, že
B = p/q, kde
p je celé číslo a q je přirozené číslo. Pak můžeme psát
xp/q = (x1/q)p
a vidíme, že taková mocnina je vlastně složením q-té odmocniny
z x a p-té mocniny pro celočíselné p, obě funkce dobře
známe. Začneme tím, že se na ně krátce podíváme.
1. Mocniny xn pro n přirozené číslo.
Jejich definiční obor je celá reálná osa. Základní tvary jsou tvary mocnin
x, x2 (parabola) a x3. Ostatní
mocniny mají tvary podobné, sudé mocniny vypadají jako x2,
liché jako x3, jen grafy jsou natáhnuty do nekonečna, čím
větší n, tím víc je graf natáhnutý.
Je-li n sudé, pak mocnina xn je sudá funkce
omezená zdola, ale ne shora, proto není omezená. Když potřebujeme prostou
část, abychom mohli udělat inverzi (odpovídající odmocninu), omezíme ji na
interval ⟨0,∞). Je rostoucí na
⟨0,∞) a klesající na
(−∞,0⟩.
Je-li n liché, pak mocnina xn je lichá funkce
neomezená zdola ani shora (proto není omezená), je prostá a proto má inverzní
funkci (odpovídající odmocninu). Je také rostoucí na celé reálné ose.
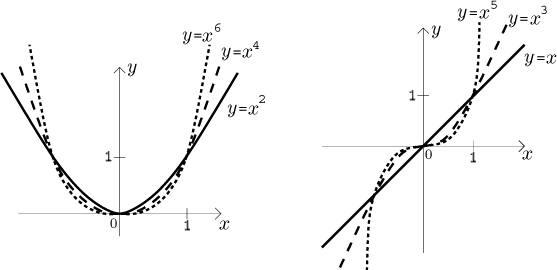
2. Pro B = 0 dostaneme konstantní funkci
x0 = 1. Její graf je vodorovná přímka. Je tedy sudá a
omezená, není prostá na žádném intervalu. Je monotonní, jmenovitě nerostoucí
a neklesající.
3. Jestliže je n záporné celé číslo, můžeme psát
n = −m, kde teď m je přirozené číslo, a
xn = 1/xm.
Hned
vidíme, že definiční obor jsou všechna reálná čísla kromě nuly. Další
vlastnosti následují z toho, co už jsme viděli. Je-li m sudé, pak
1/xm je sudá funkce omezená zdola ale ne shora,
proto není omezená. pokud potřebujeme prostou část na udělání inverze
(odpovídající odmocnina), omezíme funkci na interval
(0,∞). Funkce je klesající na
(0,∞) a rostoucí na
(−∞,0).
Je-li m liché, pak 1/xm je lichá funkce,
která není omezená zdola ani shora (tudíž není omezená), je prostá a proto má
inverzní funkci (odpovídající odmocninu). Je také klesající na
(−∞,0) a na
(0,∞).
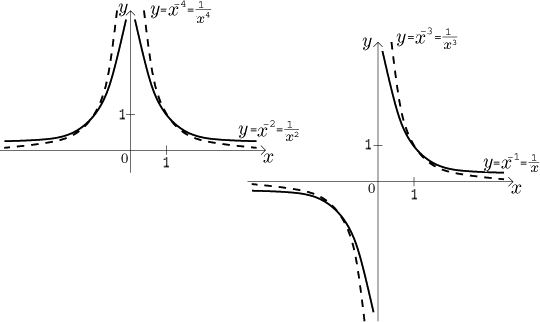
4. Jestliže B = 1/n, kde n je přirozené
číslo, pak definujeme funkci x1/n jako n-tou
odmocninu z x, tj. jako inverzní funkci k
xn.
Vlastnosti této funkce tedy plynou z vlastností
xn
pro n přirozené číslo, viz výše, mimo jiné závisí na paritě n.
Je-li n sudé, pak definiční obor je
⟨0,∞).
Funkce je omezená zdola ale ne shora (proto není
omezená), je rostoucí. Je-li n liché, pak definiční obor je celá
reálná osa, funkce není omezená, je lichá a rostoucí.
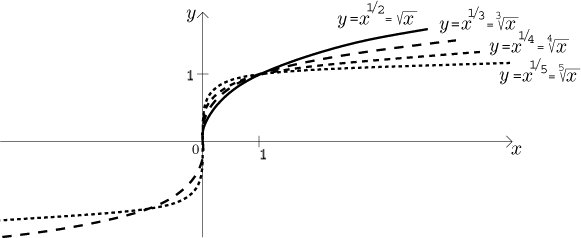
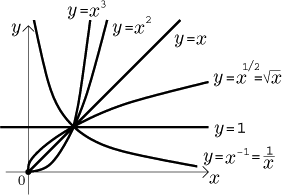
Konečně se dostáváme k důležitému případu
xp/q = (x1/q)p.
Z předchozí analýzy vyplývá, že chování této funkce závisí na dvou věcech, na
znaménku p a na paritě q.
Jestliže je p kladné a q sudé, pak definiční obor je
⟨0,∞). Funkce je omezená zdola
ale ne shora (tudíž ani omezená), je rostoucí. Je-li p kladné a
q liché, pak definiční obor je celá reálná osa, funkce není omezená,
je lichá a rostoucí. Jestliže je p záporné a q sudé, pak
definiční obor je
(0,∞).
Funkce je omezená zdola, ale ne shora (proto není omezená), je klesající.
Je-li p záporné a q liché, pak definiční obor jsou všechna
reálná čísla kromě 0, funkce není omezená, je lichá a klesající na
(−∞,0) a na
(0,∞). V následujícím
obrázku jsme každou kategorii representovali typickým příkladem.
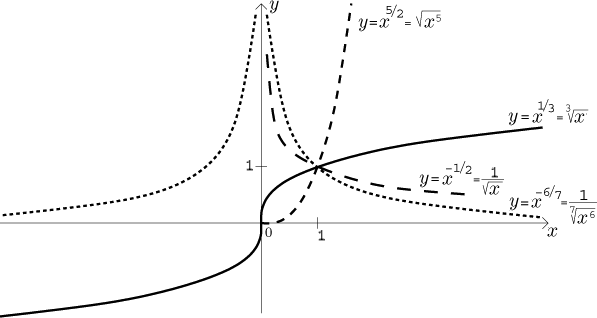
Polynomy, racionální lomené funkce
Zpět na Teorie - Elementární
funkce