Definice.
Pod pojmem polynom rozumíme libovolnou funkci ve tvaru
p(x) = a0 + a1x + a2x2 +...+ anxn, kde
ak jsou reálná čísla.
Uvažujme polynomp(x) = a0 + a1x + a2x2 +...+ anxn. Definujeme stupeň p, značenýst(p), jako největší index k splňujícíak ≠ 0.
To, že jsou ak reálné, se občas zdůrazní názvem "reálný polynom". Jsou také jiné polynomy, například "komplexní polynomy" dostaneme, když dovolíme ak, aby byly komplexní. Zde ale pracujeme pouze s reálnými funkcemi, tak budeme říkat "polynomy" a myslet tím reálné polynomy.
Čísla ak se jmenují koeficienty. Některé z nich
mohou být nula, což znamená, že vyjádření polynomu není pro daný polynom
jednoznačné. Například můžeme mít
Jaký stupeň má nulový polynom? Nejčastější volby jsou
Často používáme frázi "nechť
Pojem stupeň polynomu splňuje následující vlastnosti:
(i)
(ii)
(iii) pokud
Tyto vzorce určitě platí pro nenulové polynomy. Jejich obecná platnost
závisí na tom, jak definujeme stupeň nulového polynomu. Pokud jej nastavíme
jako
Ve většině situací stačí pouze uvažovat polynomy s
Polynom q je téhož stupně jako p a nejdůležitější vlastnosti polynomů souhlasí pro p a q, takže pak stačí zkoumat q (a ten už má koeficient u nejvyšší mocniny roven 1).
Tvar polynomu.
Pro porozumění polynomům pomůže fakt, že když je x blízko nekonečna
(nebo mínus nekonečna), pak vedoucí mocnina vždy vyhraje nad ostatními členy
- přestanou být důležité. Polynom stupně n má tedy okolo "konců",
pro velké (v absolutní hodnotě) hodnoty x, tvar velmi podobný tvaru
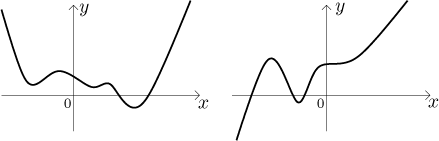
Zde jsou typické tvary polynomů sudého stupně (nalevo) a lichého stupně (napravo), za předpokladu, že je u vedoucí mocniny kladný koeficient.

Pokud je tam záporný koeficient (jako třeba u polynomu
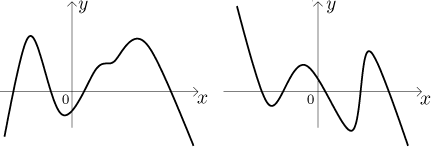
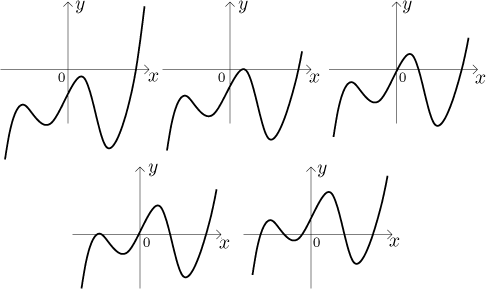
Kolik "zatáček" můžeme u polynomu p mít? Nejvíce
Z typického tvaru také vyplývá, že polynom lichého stupně musí mít sudý počet obrátek, protože jeho "konce" v nekonečnu a mínus nekonečnu vždy ukazují opačnými směry. Naopak u polynomů sudého stupně ukazují "konce" stejným směrem, proto musí mít lichý počet obrátek. Například polynom stupně pět může mít tyto základní tvary:
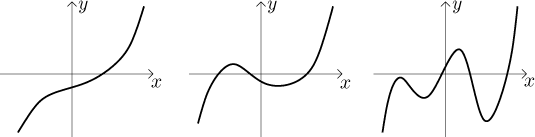
Lineární funkce.
Pod pojmem lineární funkce rozumíme libovolnou funkci ve tvaru
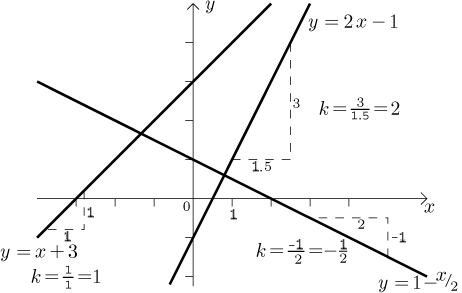
Úhel, pod kterým přímka jde, je dán vzorcem
Schopnost přecházet rychle od lineární funkce k jejímu grafu a z grafu-přímky ke vzorci, který ji dává, může být velmi užitečná, protože lineární funkce patří mezi nejužitečnější a nejčastěji se vyskytující funkce.
Kořeny polynomu.
Kolik může mít polynom p kořenů? Připomeňme, že pod slovem
kořen rozumíme číslo c splňující
Vidíme, že může mít mezi 1 a 5 kořeny. Vlastně polynomy lichého stupně mají vždy alespoň jeden reálný kořen.
Poznámka stranou: Tvrzení o počtu kořenů by platilo pro všechny polynomy, pokud bychom se rozhodli, že nulový polynom má stupeň nekonečno, ale to by způsobilo takový průšvih u jiných vlastností, že to lidé nedělají.
V komplexním oboru se polynomy chovají lépe. Krátce se tedy podíváme na komplexní věci, ale rychle se zase vrátíme do reálu. Všimněte si, že reálné polynomy jsou také komplexními polynomy, protože reálná čísla jsou podmnožinou komplexních. Když tedy máme reálný polynom, můžeme za x začít dosazovat komplexní čísla a předstírat, že je to komplexní polynom, využít pak nějaké vlastnosti. Začneme rovnou s hlavním výsledkem.
Věta.
Každý polynom (reálný či komplexní) stupně alespoň 1 má vždy nějaký komplexní kořen.Fakt (faktorizace).
Nechť c je kořen polynomu p. Pak existuje polynom q splňujícíst(q) = st(p) − 1 takový, že
p(x) = (x − c)⋅q(x).
Tento Fakt funguje obecně pro komplexní polynomy a komplexní kořeny, ale pokud začneme s reálným polynomem a reálným kořenem, pak ten nový polynom q bude taky reálný.
Pokud pracujeme v komplexních číslech, pak začneme Větou, aplikujeme Fakt o faktorizaci, a pokud není ten nový polynom q konstantní, můžeme se vrátit ke Větě a zase faktorizovat a tak dále, takže dostaneme
Důsledek (rozklad polynomu na lineární faktory).
Nechťp(x) = anxn + an−1xn−1 +...+ a1x + a0 je polynom stupněn > 0. Pak existují komplexní číslac1,c2,...,cn, která jsou všechna kořeny p a splňují
p(x) = an(x − c1)⋅(x − c2)⋅...⋅(x − cn).
Každý nenulový polynom má tedy tolik komplexních kořenů, kolik je jeho stupeň (tohle funguje i pro stupeň nula), ale některé z těchto kořenů mohou být stejné. Když dáme shodné kořeny k sobě, můžeme ten rozklad přeorganizovat na
Zde di jsou rozdílné kořeny p. Pro každý z nich se odpovídající mocnina n(i) jmenuje násobnost kořenu di (viz tato poznámka). Například můžeme mít
Pak řekneme, že 1 je kořen násobnosti 2, zatímco 3 je kořen násobnosti 1, také zvaný jednoduchý kořen.
Poznamenejme, že dostat takto pěkný rozklad s reálnými koeficienty je otázkou štěstí, protože obecně máme zaručeny pouze komplexní kořeny. Protože nás zajímají pouze reálné polynomy, zkusíme teď vydolovat něco užitečného, co by nepoužívalo komplexní čísla.
Fakt.
Jestliže c je komplexní kořen reálného polynomu p, pak jeho komplexně sdružené číslo je také kořenem p.
To je skvělé, protože to znamená, že při faktorizaci polynomu dostaneme pro
každý člen
Fakt.
Pro komplexní číslo c a jeho komplexně sdružené číslo c* máme(x − c)⋅(x − c*) = x2 + ex + f, kde e a f jsou reálná čísla.
Když tedy máme reálný polynom, můžeme dostat komplexní kořeny, ale jejich faktory lze dát dohromady po párech tak, že vytvoří reálné kvadratické polynomy. Dostaneme tedy toto:
Důsledek.
Každý reálný polynom lze napsat jako
p(x) = an(x − d1)n(1)⋅...⋅(x − dN)n(N)⋅(x2 + e1x + f1)m(1)⋅...⋅(x2 + eMx + fM)m(M), kde di, ej a fj jsou reálná čísla.
V tomto rozkladu lineární členy
Takový rozklad může být velmi užitečný a taky jsme viděli, že mít jej je ekvivalentní tomu, že známe kořeny p. Bohužel, najít takový rozklad je obecně většinou nemožné. Každé dítě zná slavný kvadratický vzorec pro nalezení kořenů kvadratického polynomu. Jsou také vzorce pro kořeny kubického polynomu (stupeň 3), ale nejsou moc pěkné a stejně si je nikdo nepamatuje. Vzorce pro polynomy stupně 4 jsou tak odporné, že většina knížek je ani neuvádí, aby nezpůsobily trauma delikátnějším čtenářům. K dovršení všeho je jedním z nejdůležitějších výsledků obecné algebry věta, že pro polynomy stupně 5 a víc ani žádné vzorce pro kořeny být nemohou.
Nalezení kořenů je proto otázkou náhody a štěstí. Obvykle zkusíme jeden kořen
uhodnout, pak vytkneme odpovídající faktor
Příklad: Zkusíme rozložit p(x) = x6 − 3x4 + 2x3.
Řešení: Vidíme, že
Vidíme tedy, že 0 je kořenem p násobnosti 3. Co teď s
Dostali jsme kvadratický polynom, jehož kořeny jsou 1 a −2 podle kvadratického vzorce. Proto je 1 vlastně kořenem násobnosti 2 a −2 je jednoduchý kořen. Dostaneme
Poznámka: Místo použití kvadratického vzorce jsme také mohli zkusit rozklad uhodnout, viz tato poznámka.
Příklad:
Zkusíme rozložit
Řešení: Zkusíme uhádnout kořen, po chvíli bychom měli dostat
Kvadratický vzorec ukazuje, že
Příklad:
Zkusíme rozložit
Řešení: Zkusíme dosadit 0, 1, −1, 2, −2,..., ale po nějaké době to vzdáme. Co můžeme dělat? Protože hádání nepomohlo, tento problém není řešitelný metodami, které známe.
Připomeňme, že jediné ireducibilní polynomy jsou ty stupně 1 (lineární) a 2 (kvadratické), takže nějaká faktorizace p musí existovat. Možná máme reálné kořeny, ale nejsou to celá čísla, a tak je neumíme uhodnout. Protože polynom je sudého stupně, může se také stát, že žádné reálné kořeny nejsou. A přesně to je pravda, máme
Jak jsme to dostali? Podvodem, tento příklad jsme vytvořili tak, že jsme začali s dvěma ireducibilními kvadratickými polynomy a vynásobili jsme je. Kdybychom tu odpověď od začátku neznali, tak bychom nevěděli, jak to vyřešit.
Teď se podíváme na trochu jiné téma, které je blízké rozkladu. Používali jsme
dělení polynomů, obecně dostaneme při dělení zbytek. Abychom měli nějakou
motivaci, připomeňme si následující: Když zkusíme vydělit 17 číslem 5,
dostaneme odpověď: Je to 3, zbytek 2. Můžeme to zapsat takto:
Je zajímavé, že přesně totéž lze udělat s polynomy, jen namísto velikosti čísla použijeme stupeň polynomu.
Fakt (dělení se zbytkem).
Nechť p,q jsou polynomy. Pak existují jednoznačně určené polynomy s,r splňující
p(x) = s(x)⋅q(x) + r(x) a
st(r) < st(q).
Můžeme to zase vyjádřit takto:
Poznámka stranou: Nemíme tu ve větě omezení na p a q, takže
jeden či oba mohou být nulové polynomy. Tento fakt zůstává pravdivý, pokud
stupeň nulového polynomu definujeme záporný, takže obě populární volby
Racionální lomená funkce či lomená funkce je libovolný zlomek
Poznámka: Lze se také setkat s názvem "racionální lomená funkce", což není moc logické, protože "racionální" znamená "lomená". Ale ono se to tak vžilo, že se obávám, že to tu v Math Tutoru mám porůznu taky.
Každou racionální funkci lze napsat jako součet polynomu a ryzí racionální funkce s týmže jmenovatelem. To je vlastně jen přeformulování Faktu o dělení se zbytkem. V praxi to děláme pomocí algoritmu pro dělení polynomů.
Protože s polynomy se pracuje relativně snadno, vidíme, že abychom uměli pracovat s racionálními funkcemi, v mnoha situacích stačí umět pracovat s ryzími racionálními funkcemi. To obzvláště platí o metodě rozkladu na parciální zlomky. Protože je tato metoda velmi důležitá, věnovali jsme jí speciální sekci, a protože jejím hlavním užitím (alespoň pro nás) je integrace, dali jsme tu sekci tam, takže pro parciální zlomky se podívejte na část Integrály - Teorie - Metody intergace - Parciální zlomky.
Stručně, metoda zahrnuje nejprve rozklad jmenovatele q na lineární a kvadratické (pokud je třeba) faktory jak jsme viděli výše, ryzí racionální funkci pak lze rozbít na součet tak zvaných parciálních zlomků, velmi jednoduchých zlomků, jejichž jmenovatelé vychází z lineárních a kvadratických faktorů q. Praktický pohled je zde.
Poslední poznámka: Když jsme probírali polynomy, zmínili jsme se, že když je
x blízko nekonečna (nebo mínus nekonečna), pak je polynom v zásadě
roven svému vedoucímu členu. Proto když je