Int(x) a Frac(x)

Definice.
Nechť x je reálné číslo. Definujeme jeho celou část jako to největší celé číslo Int(x) splňující podmínku Int(x) ≤ x.
Definujeme jeho zlomkovou část jako Frac(x) = x − Int(x).

Příklady: Int(3) = 3, Frac(3) = 0; Int(0.14) = 0, Frac(0.14) = 0.14; Int(17/8) = 2, Frac(17/8) = 1/8 = 0.125; Int(85263.781235) = 85263, Frac(85263.781235) = 0.781235.
Teď to bude zajímavější: Int(−1) = −1, Frac(−1) = 0; Int(−2.15) = −3 (opravdu, −3 je největší celé číslo, které nepřeleze −2.15), Frac(−2.15) = 0.85; Int(−135.643) = −136, Frac(−135.643) = 0.357; Int(−117) = −117, Frac(−117) = 0.

Asi se teď ptáte, proč jsme nedefinovali Int(x) jako to, co je před desetinnou čárkou, a Frac(x) jako to, co je za ní. To je dobrá otázka, mi by se to také tak líbilo. Bohužel, taková definice by občas působila problémy, zatímco ta srandovní, kterou tady máme, je z matematického hlediska bezproblémová. Jednu výhodu ukážeme hned: Ta "správná" definice dává mnohem hezčí grafy:

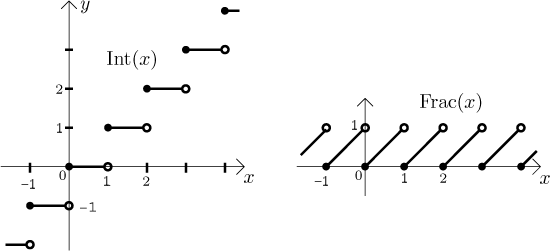
Vzhledem k tomu, že tyto funkce používáme většinou pro kladná čísla, spousta lidí ani neví, že se tyto definice chovají srandovně pro záporná čísla.

Existuje další odůvodnění pro právě tuto definici. Můžeme říct, že Int(x) je vlastně x zaokrouhlené dolů na nejbližší celé číslo. Existuje i alternativní zápis, Int(x) = ⌊x⌋. Podobně definujeme ⌈x⌉ jako x zaokrouhleno nahoru na nejbližší celé číslo.

Příklady: ⌊13⌋ = 13, ⌈13⌉ = 13; ⌊13.7⌋ = 13, ⌈13.7⌉ = 14; ⌊−23⌋ = −23, ⌈−23⌉ = −23; ⌊−23.6⌋ = −24, ⌈−23.6⌉ = −23.

Faktoriál
Zpět na Teorie - Elementární funkce