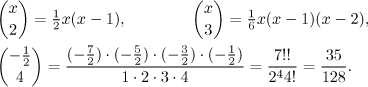Faktoriál není vlastně reálná funkce (viz níže), ale je tak důležitý, že jsme jej zahrnuli sem mezi užitečné funkce.
Definice.
Nechť k je přirozené číslo. Definujeme jeho faktoriál jako
k!=1⋅2⋅3⋅...⋅(k − 1)⋅k. Také definujeme
0! = 1.
Příklady:
Faktoriál roste velmi rychle, například
Důležitá vlastnost faktoriálu je, že se radostně krátí ve zlomcích. Například:
![]()
Podobně
![]()
Nevýhoda je, že nemá žádné pěkné algebraické vlastnosti, například nejsou
žádné pěkné formulky pro výrazy jako
Takové výrazy jsou častým zdrojem chyb při krácení, zde je jeden správný příklad:
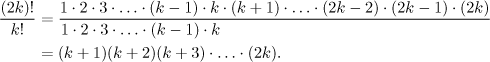
Nic víc se s tím nedá dělat.
Existuje věc zvaná dvojný factoriál, kde se namísto násobení všech čísel bere jen každé druhé.
Definice.
Nechť k je přirozené číslo. Definujeme k!! jako
k!! = 1⋅3⋅5⋅...⋅(k − 2)⋅k pro k liché,
k!! = 2⋅4⋅6⋅...⋅(k − 2)⋅k pro k sudé.
Příklady:
Faktoriál je funkce, jejímž definičním oborem jsou přirozená čísla a nula. Je možné tuto definici rozšířit na větší množinu (třeba na všechna nezáporná čísla) jakýmsi propojením bodů v grafu? To by bylo velmi užitečné, například bychom mohli používat l'Hospitalovo pravidlo pro limity s faktoriály. Dobrá zpráva je, že odpověď je kladná, existuje funkce definovaná na všech reálných číslech s výjimkou záporných celých čísel, která se shoduje s faktoriálem v přirozených číslech, viz gama funkce. Špatná zpráva je, že s touto funkcí se nepracuje zrovna snadno, mimo jiné ty triky, které jsme si ukázali pro hledání limit, se vypořádají s faktoriály mnohem lépe, než kdybychom blbli s gama funkcí.
Definice.
Nechť n ≥ k jsou nezáporná celá čísla. Definujeme
Říká se tomu kombinatorické číslo, kombinační číslo, binomický koeficient či binomické číslo. Výraz čteme "n nad k".
Příklad:
![]()
Pár identit:
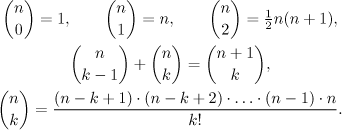
Poslední identita je velice zajímavá, protože na její pravé straně nejsou nahoře žádné faktoriály, jinými slovy, proměnná n se může měnit dle libosti. Můžeme tak uvést užitečné zobecnění.
Definice.
Nechť x je reálné číslo, k přirozené číslo. Definujeme kombinatorické číslo vztahem
Příklady: