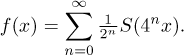"Pilovité" funkce
V této sekci se podíváme na některé funkce ze "zoo příšerek", které nám
poslouží jako varování, že některé nápady, i když mohou vypadat správně, když
uvažujeme "pěkné" obrázky, nemusí ve skutečnosti fungovat. Máme mnoho
takových užitečných "protipříkladových" funkcí, zde se podíváme na ty, které
v sobě mají jakousi "pilovitou" ideu.
Příklad 1
Uvažujme následující funkci na intervalu (0,1⟩. Nejprve vezmeme interval
⟨1/2,1⟩ a vztyčíme nad ním
pravidelný "zub" o výšce 1/2, tj. představíme si rovnostranný trojúhelník se
základnou ⟨1/2,1⟩ a výškou
1/2. V dalším kroku
se podíváme na to, co zbylo z (0,1⟩,
jmenovitě (0,1/2), a vezmeme jeho pravou polovinu.
Na intervalu ⟨1/4,1/2⟩ vztyčíme další "zub" o výšce
1/2. Dále se podíváme na to, co zbylo, jmenovitě
(0,1/4), a vztyčíme "zub" o
výšce 1/2 nad pravou polovinou, ⟨1/8,1/4⟩.
Pokračujeme tímto způsobem, nakonec (po nekonečně mnoha krocích) uděláme zuby
nad celým intervalem (0,1⟩.
Funkce, kterou jsme takto dostali, je spojitá na
(0,1⟩, je
omezená, ale přesto nemá limitu v 0 zprava.
Modifikace 1:. V každém kroku uděláme zub jako předtím, ale teď budeme
dělat jeho výšku vždy polovinu výšky předchozí, takže první zub bude mít
výšku 1/2, druhý 1/4 atd. Náhodou to tak vychází, že když děláme zub nad
určitým intervalem, tak je jeho výška stejná jako levý konec tohoto intervalu
(ověřte).
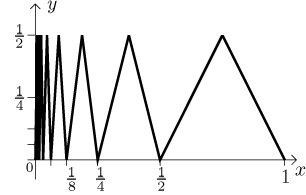
Tato funkce, nazvěme ji f, splňuje
| f (x)| ≤ x, proto podle
Věty o sevření má
limitu v 0 zprava, jmenovitě nulu (mělo by to být jasné z obrázku).
Můžeme proto také definovat f (0) = 0 a dostaneme funkci na
⟨0,1⟩, která je spojitá.
Mimochodem kdybychom chtěli být přesní (za chvíli to použijeme), můžeme
ukázat, že vrcholy zubů leží na přímce
y = (2/3)x.
Teď vezmeme tento příklad a "zrcadlíme" jej na interval
⟨−1,0⟩ symetricky vzhledem k
počátku, tj. překlopíme graf okolo osy y a pak okolo osy x.
Pořád tomu budeme říkat f, protože je to jen prodloužení předchozího
obrázku.
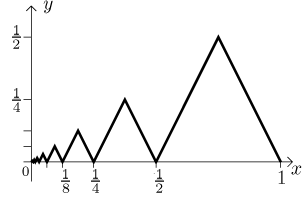
Tato funkce je spojitá a lichá na ⟨−1,1⟩,
všimněte si, že je neklesající v 0, ale vůbec neexistuje interval, na
kterém by tato funkce byla monotonní a který by obsahoval 0 ve svém
vnitřku. Ať už zvolíme jakýkliv interval (a,b), pokud máme
a < 0 a
b > 0, pak tento interval bude obsahovat nějaký zub,
což znamená, že funkce tam někde půjde nakoru a zase dolů uvnitř
(a,b), čímž tam zničí jakoukoliv monotonii.
Všimněte si také, že tato funkce nemá derivaci v počátku,
ačkoliv je tato funkce spojitá a monotonní v
x = 0. Jen si
zkuste vzít nějaké nenulové y a uvažujte přímku spojující počátek s
bodem (y, f ( y)). Co se stane se směrnicí této přímky,
když pošleme y do 0? Jakkoliv blízko k 0 se dostaneme, vždy budou
ještě blíže nějaké hodnoty, kde zuby klesnou na osu x, tj. kde
f ( y) = 0, pak je směrnice 0. Na druhou stranu, budou
tam také vždy vrcholky zubů, kde je směrnice 2/3 (viz poznámečka před
chvílí). Když tedy posíláme y do 0, směrnice nepřestávají oscilovat
mezi 0 a 2/3, proto nemají limitu.
Modifikace 1*:. V předchozím obrázku leží vrcholky zubů na přímce
y = 2x/3. Můžeme modifikovat definici tak, aby
vrcholky zubů sledovaly pro kladné x parabolu
y = x2 a na záporné části opět zrcadlíme
tu kladnou:
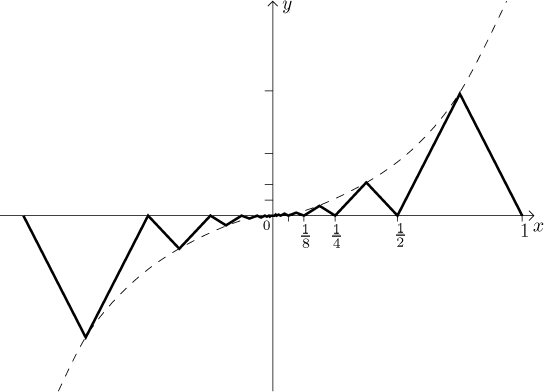
Tato funkce má podobné vlastnosti jako ta z Modifikace 1, ale teď má dokonce
derivaci v x = 0, je rovna nule.
Modifikace 2: Vezmeme funkci z Modifikace 1 a uděláme malou změnu:
přehodíme každý druhý zub (počítáno od konců) okolo osy x.
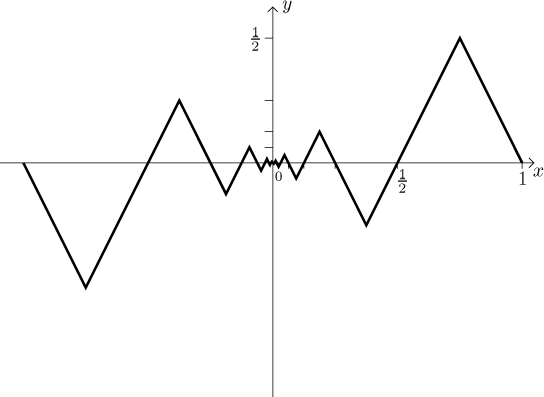
Zase máme spojitou a lichou funkci na ⟨−1,1⟩
bez derivace v 0, ale tentokráte nemáme v 0 ani žádnou monotonii.
Příklad 2
Není to vlastně ani "pilovitá" funkce, ale dostaneme ji pohodlně z
předchozího příkladu. Vezměme funkci f z Modifikace 1 a udělejme
následující změnu (popíšeme pravou polovinu, levá je symetrická): Uvažujme
interval I, nad kterým byl vztyčen zub (třeba
⟨1/2,1⟩,
⟨1/4,1/2⟩,
atd). Namísto zubu
nakreslíme vodorovnou čáru na úrovni vrcholku zubu, ale pouze nad pravou
polovinou tohoto intervalu (kde šel zub dolů), a také vodorovnou čáru na
úrovni čtvrtiny výšky zubu nad levou polovinou (kde šel zub nahoru).
Vybarvíme konce, které jsou blíže k počátku (a taky ty úplně vnější).
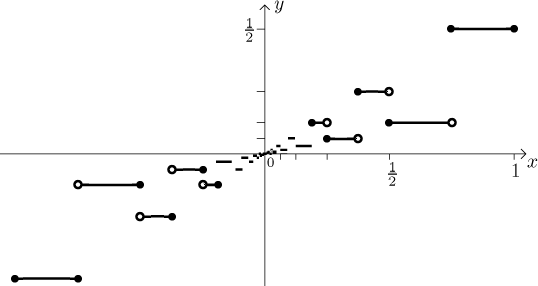
Toto je docela zajímavá funkce. Všimněte si, že stále
| f (x)| ≤ |x| pro všechna x z
⟨−1,1⟩,
takže má tato funkce limitu 0 v x = 0, je proto v nule
spojitá. Tato funkce je také monotonní v 0, tentokráte dokonce (striktně)
rostoucí.
Nemáme ale žádný interval okolo počátku, kde by tato funkce byla
monotonní, a není také žádný takový interval, kde by byla
spojitá. Toto ukazuje, že monotonie a spojitost v bodě nezaručují, že
funkce bude mít nějaký interval okolo dotyčného bodu, kde by byla "pěkná"
(monotonní nebo spojitá).
I v tomto příkladě nemáme derivaci v 0. Není těžké ukázat, že tentokráte
směrnice příslušných přímek oscilují mezi 2/3 a 1/6.
I tento příklad se dá upravit tak, aby měl derivaci v počátku (viz předchozí
modifikace 1*). Vznikne tak funkce, která má derivaci v počátku, ale
neexistuje žádné okolí počátku, na kterém by byla spojitá či monotonní.
Hlavně s tou spojitostí to je smutné, vidíme, že existence derivace v bodě
nepřinutí funkci, aby byla pěkná trochu kolem. Pokud vás to zajímá, připojíme
podrobnosti o konstrukci. Úsečky jsme v modifikaci 1* dělali po párech a ta
napravo ("horní") měla levý konec na křivce
y = 2x/3
(pro kladná x, levá půlka grafu byla symetrická). Modifikace spočívá v
tom, že teď páry děláme tak, aby ty "horní" úsečky (z pravé půlky grafu) měly
levý konec na křivce y = x2, každá "dolní"
úsečka teď bude na úrovni jedné šestiny odpovídající "horní" úsečky.
Příklad 3
Teď zkusíme něco jiného. Vytvoříme funkci na
⟨0,1⟩,
která není omezená. Nápad
je podobný. Nejprve uděláme zub výšky 1 nad
⟨1/2,1⟩.
Pak uděláme zub výšky 2 nad
⟨1/4,1/2⟩. Pak uděláme zub výšky 4 nad
⟨1/8,1/4⟩. Pokračujeme tímto způsobem,
pokaždé zdvojnásobíme výšku zubu. nakonec pokryjeme
(0,1⟩, takže zbývá definovat
funkci v 0. To můžeme udělat, jak se nám zlíbí, například určíme hodnotu v 0
jako 1 (obrázek je tak přecpaný, že to tam stejně nebude vidět).
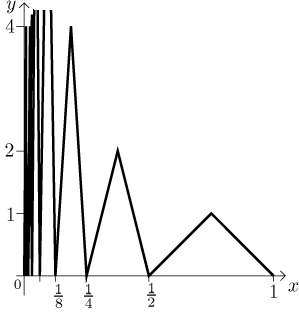
Tato funkce je definovaná na omezeném intervalu
⟨0,1⟩, ale není
omezená shora, jen zdola.
Když uděláme malou modifikaci a necháme jít každý druhý zub dolů, dostaneme
funkci, která nebude ani omezená zdola.
Příklad 4
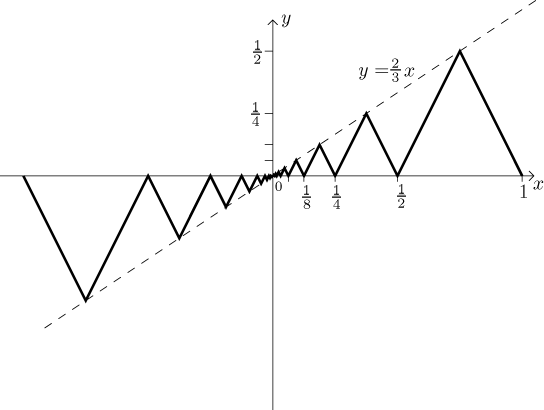
Zde použijeme nekonečnou sumu k vytvoření funkce na
ℝ. Začneme jednoduchou
pravidelnou "pilou", to bude funkce S:
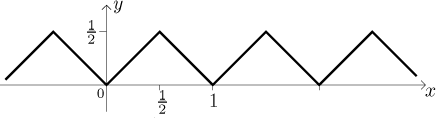
Druhá funkce bude S celá zmenšená čtyřikrát a pak vynásobená dvěma,
nazvěme ji S2:
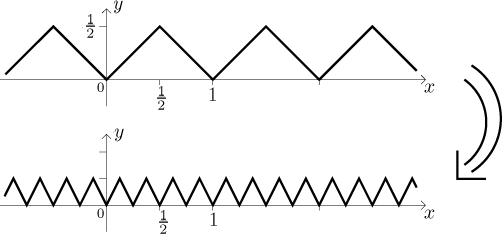
Každý zub byl tak rozložen na čtyři, jejichž výšky jsou polovina výšky
původního zubu. Všimněte si, že zuby jsou tak dvakrát příkřejší než ty
původní. Matematicky můžeme psát
S2(x) = S(4x)/2.
Všimněte si, že obě tyto funkce jsou 1-periodické, totéž bude platit i o
ostatních, proto se zaměříme na jednu periodu.
V dalším kroku vytvoříme S3 zmenšením celé funkce
S2 čtyřikrát a vynásobením dvěma:
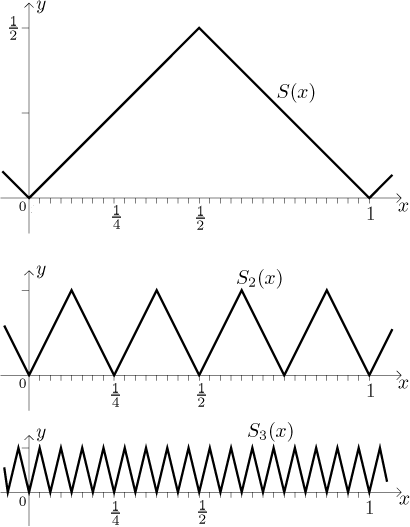
Teď
S3(x) = S2(4x)/2 = S(42x)/22.
Pokračujeme tímto způsobem, dostaneme tak funkce
Sn(x) = S(4nx)/2n.
Co se stane, když je sečteme? To dá trochu práce
(viz Funkční řady
v části Řady - Teorie), ale dá se ukázat, že tento nekonečný součet má smysl
(konverguje) a dává spojitou funkci. Můžeme tedy definovat
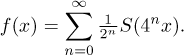
Jak to vypadá? Pořád kreslíme jen jednu periodu:
Když přidáme S2 k S, dostaneme toto:
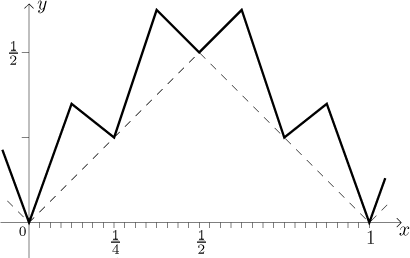
Všimněte si následující věci. Za prvé, na každé ploché části grafu S
vyrostly dvě pyramidy. Za druhé, funkce S neměla derivace v bodech
ve tvaru k/2 a teď, po přičtení S2, nemá součet
derivace v bodech ve tvaru
k/(2⋅4) = k/8.
Teď přidáme S3.
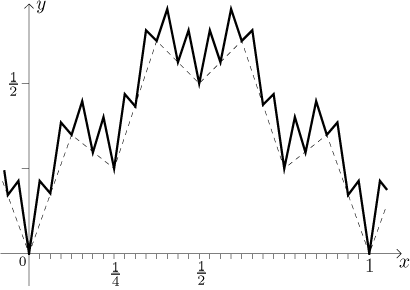
Všimněte si, že trendy se zachovávají. Na každé ploché části vyrostly dvě
pyramidy a nejsou derivace v bodech ve tvaru
k/(8⋅4) = k/32. Po přičtení
S4 dostaneme
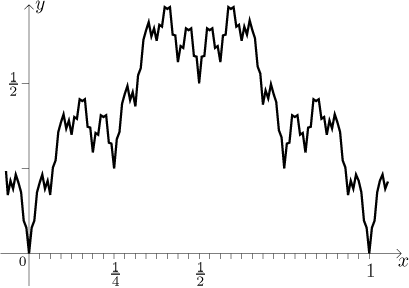
Pokračujeme tímto způsobem a dostaneme funkci f. Protože jsou pyramidy
stále tenčí a tenčí, brzy nedokážeme graf pořádně nakreslit, to nejlepší, co
se dá říct, je, že to bude v zásadě jako ta pyramida nahoře, ale rozmazanější.
Co je důležitější, dá se dokázat, že dalším přičítáním pyramid se nenapraví
"zlomové" body, kde nebyly derivace. Funkce f proto
nemá derivace v bodech ve tvaru k/2n.
To je ale docela špatné, protože tyto body jsou husté na reálné ose, jsou
úplně všude. Máme tedy funkci spojitou na reálné ose, ale není jediný
nedegenerovaný interval, na kterém by měla derivaci.
Co je zajímavé, matematici použili stejný nápad, aby vytvořili monstrózní
funkci, která je spojitá na celé reálné ose, ale nemá derivaci vůbec nikde,
dokonce ani nemá vlastní jednostranné derivace! Těžko se to představuje, ale
teď tomu alespoň můžete věřit. Vlastně jde o konstrukci obdobnou, jako jsme
teď viděli, začne se stejnou funkcí S a pak se přičítají
Sn(x) = S(100nx)/10n.
Proč jsme to tedy neukázali rovnou? Protože bychom to nemohli tak dobře
nakreslit, všimněte si, že už funkce S2 má 100 malinkých
pyramidek na intervalu (0,1).
sin(1/x) a spol.
Zpět na Teorie - Elementární funkce